Third Problem set

1. Plot the director field and the solution curves for the equation
   

   $$\frac{d}{dx} y(x) = x^2.$$
   
   

2. In the following equations circle all properties that are true

   ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations

   1. 
      
      $$\dot x(t) = x(t),$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations
      
   2. 
      
      $$\dot x(t) = x(t)^2,$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations
      
   3. 
      
      $$\dot x(t) = x(t)^3+34,$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations
      
   4. 
      
      $$y''(x) = x^2 y(x),$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations
   5. 
      
      $$y''(x) = x^2 y^2(x),$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations

   6. 
      
      $$\frac{\partial}{\partial x} U(x,t) = \frac{\partial}{\partial t} U(x,t),$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations
   7. 
      
      $$\frac{\partial}{\partial x} U(x,t) = \frac{\partial}{\partial t} (U(x,t))^3,$$
      
      
      ODE ,PDE , Linear , Nonlinear, First Order , Second Order, Third Order, Homogeneous, Non-homogeneous, Single Equation, System of Equations

3. In this problem, please write down examples of the Differential Equation that are

   • Linear Homogeneous Ordinary Differential Equation of the first order
   • Nonlinear Homogeneous Ordinary Differential Equation of the first order
   • Linear Second Order Linear Differential Equation with Constant coefficients
   • Partial Differential Equation

   DO NOT SOLVE THESE EQUATIONS

4. During the darkest period of the History of Magic, the Death Eaters movement of followers of Lord Voldemort was gaining momentum fast. The rate of growth of a number of Death Eaters is proportional to the amount of Death Eaters. In the absence of other factors, the number of Death Eaters tripples every two days. One Death Eater is converted to the Order of the Phoenix every day (i.e. stops being Death Eater). Assuming that at time $t=0$ there were only five Death Eaters, calculate the amount of Death Eaters in a week.

   Extra Credit 10 percent What happens with the number of the Death Eaters as $t\to\infty$? If the number of Death Eaters becomes too large, please modify the equation to give the Order of the Phoenix (the good guys) the chance of victory.

5. Ten years ago, an industrial company built a factory in a pristine valley. The valley's volume is $10^6\;m^3$. The factory started spewing $100\; kg/year$ of pollutants through smoke stacks with volume flow $10^5\;m^3/year$. Well-mixed polluted air leaves the valley at the same rate. What is the concentration of the pollutants in the valley now?

   1. Write ODE
   2. Solve ODE
   3. Satisfy IC
   4. Find concentration now

   HINT: Use the approximate value 1/3 for $1/e$.

6. The volume of a lake oscillates yearly as $V=V_0(2-\cos\omega t)$, where $\omega$ = $2\pi$ year$^{-1}$, and $t$ is measured from January 1, 2001. A creek with flow rate $\Phi$ flows into the lake. On January 1, 2001, a new farm began operating near this creek and spilling refuse into it. The concentration of this refuse in the creek water is $c=c_0(1+\sin\omega t)$. Well-mixed polluted water leaves the lake at the same rate $\Phi$. Write down the initial-value problem that describes the pogllution level, i.e., mass of the refuse, $M$, in the lake. Do not solve it.

7. The amount $Q$ of a imagination improving drug in a student bloodstream diminishes at a rate proportional to the amount present, with proportionality constant $r$. The patient takes $k$ milligrams of the drug per day. Write the initial-value problem that describes the amount of the drug in the patient's bloodstream, if the patient started taking the drug at the time $t=0$.

   
   

8. Start up company of RPI DFQ students is testing the speed at which RPI campus can be taught to use company invention, smart DFQ-pen. Smart DFQ-pen can solve differential equations, notify user of incoming emails and phone calls, take pictures with build in digital camera, play MP3 music, and it can write too.

   The speed at which DFQ-pen gains popularity and is adopted by RPI students is proportional to the percent of students having the DFQ-pen and the percent of students not having the smart DFQ-pen. Assume that coefficient of proportionality is such that at the beginning, when almost nobody uses the smart DFQ pen, the number of people having the smart DFQ pen triples every week. Find the number of students having the smart DFQ pen as a function of time.

   Extra Credit 10 percent Assuming that initially only one person out of a hundred have the smart DFQ pen, estimate number of people using the pen in 28 days. To find a final answer, you may approximate the value of
   

   $$e =2.71828182845904523536028747135$$
   
   
   by 3.

9. In 1992, Jane was just of out college and broke when she landed a Wall street job. Her initial salary was $50 K, and kept increasing by 10% per year. She put 10% of the salary away in a mutual fund, which grew at the annual percentage rate of 20%. Formulate the initial-value problem describing the growth of Jane's mutual fund throughout the 1990's.

   HINT: You must first compute Jane's salary at any given moment.

10. ``Creative'' bartender is selling beer initially containing 5% alcohol from a 200 gallon keg at the rate of 20 gallons per hour. He has hooked up a secret hose bringing water to the keg to ``replenish" the beer. He knows that the the customers will notice the difference when the beer is diluted to one half of its original strength. After how much time does he have to disconnect the hose?

11. The number $N(t)$ of the members of the Order of Phoenix changes according to the law
    
    $$\dot N(t) = (N(t))^2 (N(t)-100)(N(t)-20).$$
    
    
    Determine the number, position, and type of the equilibria points for this equation, and draw some representative solution curves in the $tN$-plane. Which of these solutions are favorable for the Order of Phoenix mission, and which solutions are favorable to Death Eaters, and which are nonphysical.

    Hint The raise of numbers of the Order of Phoenix members are favorable to the order of Phoenix mission, decline of numbers of members of Order of Phoenix is favorable to Death Eaters.

12. The number of members of the Capital District Extreme Sky Diving association grows proportionally the number of members it is currently has. Approximately three members per year leave the association due to injuries, death or other reasons. In the absence of other factors, association triples its size every 5 years. Assuming there were 100 members in 2015, how many members will association have in 2030? (You may use calculators for this problem).

13. The speed of propagation of gossip in a closed group is directly proportional to a percentage of people knowing the gossip and is also proportional the percentage of people not knowing the gossip. Assume that coefficient of proportionality is such that at the beginning of propagation of a gossip, when almost nobody knows the gossip, the number of people knowing the gossip tripples every two days. Find the number of people knowing the gossip as a function of time.

    Extra Credit 10 percent Assuming that initially gossip is known by one person out of a hundred, estimate a fraction of people knowing the gossip in a week. To find a final answer, you may approximate the value of
    

    $$e =2.71828182845904523536028747135$$
    
    
    by 3.

    Steps to be performed to solve the problem are

    1. Write an ODE
    2. Determine coefficient of proportionality
    3. Solve ODE
    4. Satisfy IC
    5. Find fraction of people knowing a gossip in a week.

14. The population of mosquitoes in a swamp increases at a rate proportional go the current population, and in the absence of other factors, the population triples each week. There are 100000 mosquitoes in the area initially, and birds and bats eat 10000 mosquitoes daily. Determine the population of mosquitoes at a swamp at any given time.

    HINTS:

    1. Write ODE
    2. Solve ODE
    3. Satisfy IC
    4. Find analytical solution to the ODE that satisfies IC.

    Extra Credit 10 % What happens as $t\to\infty$? Propose the mechanism which leads to more realistic predictions, and how would you change the equation to model this mechanism?

15. A population $P(t)$ of squirrels of the Prospect Park in Troy NY is limited by the finate area of the part, changes according to the differential equation
    

    $$\frac{d P}{d t} = 2 P - \frac{P^2}{100},$$ (3)

    
    
    where $t$ is measured in years, and $P$ is measured in squarels.
    1. What are the equilibrium points of the population
    2. Now consider the effects of predators, which includes owls, hawks, eagles, snakes and RPI students. Suppose that the squirrels are eliminated at a constant rate of $75$ squirrels per year. Write down a modified differential equation for the squarrel population which includes the effect of predators.
    3. What are the new equilibrium levels of the population of squarrels?
    4. For the modified equation of 2, determine equilibrium points and their stability.
    5. Plot the few characteristic $P(t)$ curves for various initial conditions. Consider all possibilities
    6. Explain in words how the equilibria of the problem changes with addition of predators. In other words, explain the difference of equilibria of equation (3) and modified equation of 2.
    7. Extra Credit What is the maximum predation rate $R$ at which a nonzero squirrel population can be maintained indefinitely?

16. We have studied the integrating factor method to solve
    

    $$y'(x)+p(x)y(x)=g(x).$$ (4)

    
    
    Equation (21) is multiplied by an integrating factor
    

    $$\mu(x)=e^{\int p(x') d x'},$$ (5)

    
    
    to get
    

    $$\frac{d}{dx}(y(x)e^{\int p(x') d x'}) = g(x)e^{\int p(x') d x'},$$ (6)

    
    
    which is solved by integrating both sides. The result of this integration will be a function of an arbitrary integration constant. Therefore the general solution of (21) is a function of one arbitrary constant.

    Now suppose that function $P(x)$ is such that
    

    $$\frac{d}{d x} P(x) = p(x).$$
    
    
    Then instead of (5) we may write
    

    $$\mu(x) = e^{P(x)+C},$$ (7)

    
    
    where $C$ is an arbitrary integration constant . Then, instead of (6) we obtain
    

    $$\frac{d}{dx}(y(x)e^{P(x)+C}) = g(x)e^{P(x)+C},$$ (8)

    
    
    and integrating both sides of (8) will produce an answer which is a function of two arbitrary constants instead of one, as it should be.

    Explain and resolve this apparent contradiction

17. Consider the first order ordinary linear ordinary differential equation
    

    $$y'(x) + q(x) y(x) = 0.$$
    
    
    1. Solve this ODE by method of separation of variables
    2. Solve this ODE by method of integrating factor
    3. Compare the answers. What of the methods of solving this equation would you recommend to DFQ students?

18. Solve the initial-value problem
    

    $$(x+1)^2y'-(x+1)y=-2, \qquad y(0)=0,$$ (9)

    
    
    and sketch the solution.
    1. Solve ODE
    2. Satisfy IC
    3. Plot the solution

    Extra Credit: Sketch sufficiently many representative integral curves of the differential equation in (9) to show how all its solutions behave.

19. Find the explicit solution of the initial-value problem
    

    $$yy' + x(y^2-1)=0, \qquad y(0)=-2.$$
    
    
    HINT: The equation is separable.
    1. Solve ODE
    2. Satisfy IC

    Extra credit: Sketch this solution.

20. Find the explicit solution of the initial-value problem
    

    $$yy' + 2(x-1)^3(1+y^2)=0, \qquad y(1)=-1.$$
    
    
    HINTS:
    1. The equation is separable
    2. Solve ODE
    3. Satisfy IC

21. Solve the initial value problem
    

    $$y^{\prime }+\frac{2}{x}y={\frac{\cos x}{x^{2}}}+1,\quad y(\pi )=0.$$
    
    

22. Find the explicit solution of the initial-value problem
    

    $${\frac{dy}{dx}}={\frac{e^{x}}{2(y+1)}},\qquad y(0)=0,$$
    
    
    and sketch it.

23. Solve the initial-value problem
    

    $$(x+1)^2y'-(x+1)y=-2, \qquad y(0)=0,$$ (10)

    
    
    and sketch the solution.
    1. Solve ODE
    2. Satisfy IC
    3. Plot the solution

24. The number of bacteria in a Petri dish is governed by the equation
    

    $$\frac{dN}{dt} = -N(N-a)(N-b), \qquad 0<a<b$$
    
    
    where $a$ and $b$ are constants. Determine the number, position, and stability type of the equilibria for this equation, and draw some representative solution curves in the $tN$-plane. Which of these curves are physical and which are not?

    
    

25. Consider the problem
    

    $$\frac{dN}{dt} = a N-N^2.$$
    
    
    Sketch ${dN}/{dt}$ versus $N$, determine all possible equilibria and their stability type (stable, unstable, semi-stable), and draw some representative integral curves in the $t-N$ plane for all three cases: $a>0$, $a=0$, and $a<0$.

    HINT: If you have trouble with the abstract constant $a$, do it for $a=-1$, $a=0$, and $a=1$.

    1. Plot $\dot N$ versus N
    2. Find equilibrium points and their stability
    3. Rotate graph and draw $N(t)$
    4. Where the is maximum growth of $N$
26. For the problem $\dot u = r-u^2$, sketch $\dot u$ versus $u$, determine all possible equilibria and their stability type (stable, unstable, semi-stable), and draw some representative integral curves in the $t-u$ plane for all three cases $r>0$, $r=0$, and $r<0$.

    HINT: If you have trouble with the abstract constant, $r=1$, $r=0$, and $r=-1$ will do the trick.

27. Calculate the general solution of the equation
    

    $$y''(x)-3y'(x)+2 y(x)= e^x, %$$
    
    

28. Calculate the solution to the initial value problem
    

    $$y''(x)+y'(x)-2 y(x)= 0, y(0)=5, y'(0)=-4.$$
    
    

29. Calculate the general solution of
    

    $$y''(x)-2 y'(x)+2 y(x)= 0.$$
    
    

30. Calculate the general solution of
    

    $$(x-2)^2 y''(x)-3(x-2) y'(x)+8 y(x)= 0.$$
    
    

31. Compute the solution of the initial value problem
    

    $$y''-9y'+20y=0, \qquad \qquad y(0)=0, \quad y'(0)=1.$$
    
    

32. Calculate the general solution of the equation
    
    $$y''(x)+6 y'(x) + 9 y(x) = 0,$$
    
    
    and sketch few $y(x)$ curves for different values of arbitrary constants.

33. Compute the solution of the initial value problem
    

    $$y''+2y'+2y=0, \qquad \qquad y(\pi)=-1, \quad y'(\pi)=0.$$
    
    

34. Find the FORM of the general solution of the problem
    

    $$y'' - 2y' +y=(x^2-2x+1)e^x.$$
    
    
    Do not compute the unknown coefficients in it.

35. Calculate the general solution of the equation
    

    $$y''-2y'+y=\frac{e^x}{1+x^2}.$$
    
    

    HINT: Think carefully what method you will use for computing the particular solution of the inhomogeneous problem!

    HINT:
    

    $$\frac{d}{d x} {\rm {ArcTan}} x = \frac{1}{1+x^2}.$$
    
    

36. Find the general solution of the equation
    

    $$y''-2y'+y=e^x.$$
    
    

37. (a) Compute the general solution of the problem
    

    $$y''-2y'+y=e^x.$$
    
    

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

    (b) Find the FORM of the general solution of the problem
    

    $$y'' - 2y' +y=(x^2-2x+1)e^x.$$
    
    
    Do not compute the unknown coefficients in it.

38. Solve

    
    

    $$y''(x) - y'(x) - 6 y(x) =0, y(0)=3;y'(0)=-1.$$
    
    

    Sketch $y(t)$.

39. We have studied integrating factor method for solving general first order linear ODE. Integrating factor method can sometimes be generalized for nonlinear first order ODE's.

    Find the general solution of the following first order ODE:
    

    $$y'(x)\cdot \cos (y(x)) + \frac{\sin(y(x))}{x}= x^3.$$
    
    

    This is nonlinear ODE, so the method we studied in class can not be used directly. Yet, you can find an integrating factor, i.e. the function which can be used to multiply both Left Hand Side and Right Hand Side of this equation to make the Right Hand Side become a full derivative. You may try to use your ``regular'' integrating factor method and see what happens.

    If this fails, there exists a change of variables which makes this equation linear.

40. Find the explicit solution of the initial-value problem
    
    $$yy' + x(y^2-1)=0, \qquad y(0)=-2.$$
    
    
    HINT: The equation is separable.
    1. Solve ODE
    2. Satisfy IC

    Extra credit: Sketch this solution.

41. What is the general solution of the equation
    

    $$x^2y''-xy' +y = x.$$
    
    

42. What is the general solution of the equation
    

    $$x^2y''-xy' +y = x.$$
    
    

43. 4. Consider the problem
    

    $$\frac{dN}{dt} =N^2-2N-3.$$
    
    
    Sketch ${dN}/{dt}$ versus $N$, determine all possible equilibria and their stability type (stable, unstable, mixed, and draw some representative integral curves in the $t-N$ plane.
    1. Plot $\dot N$ versus $N$.
    2. Find equilibrium points and their stability.
    3. Rotate the graph and draw $N(t)$.
    4. Where the is maximum growth of $N(t)$
44. 4. Consider the problem
    
    $$\frac{dN}{dt} = a N-N^2.$$
    
    
    Sketch ${dN}/{dt}$ versus $N$, determine all possible equilibria and their stability type (stable, unstable, semi-stable), and draw some representative integral curves in the $t-N$ plane for all three cases: $a>0$, $a=0$, and $a<0$.

    HINT: If you have trouble with the abstract constant $a$, do it for $a=-1$, $a=0$, and $a=1$.

    1. Plot $\dot N$ versus N
    2. Find equilibrium points and their stability
    3. Rotate graph and draw $N(t)$
    4. Where the is maximum growth of $N$

45. Extra Credit 20 percent
    We have studied integrating factor method for solving general first order linear ODE. Integrating factor method can sometimes be generalized for nonlinear first order ODE's.

    Find the general solution of the following first order ODE:
    

    $$y'(x)\cdot \cos (y(x)) + \frac{\sin(y(x))}{x}= x^3.$$
    
    

    This is nonlinear ODE, so the method we studied in class can not be used directly. Yet, you can find an integrating factor, i.e. the function which can be used to multiply both Left Hand Side and Right Hand Side of this equation to make the Right Hand Side become a full derivative. You may try to use your ``regular'' integrating factor method and see what happens.

    If this fails, there exists a change of variables which makes this equation linear.

46. 1

    Solve the initial value problem
    

    $$y''(x)+4 y'(x)-21 y (x) =0, y(0) =0;y'(0)=4.$$
    
    

47. Find the general solution to the equation
    

    $$(x-2)^2 y''(x) + (x-2) y'(x) - y(x) = 0.$$
    
    

48. Solve the inhomogeneous ordinary differential equation of a second order by method of undetermined coefficients:
    

    $$2 y''(x)+ 3y'(x) + y(x)= x^2 + 3 \sin(x).$$
    
    

49. Solve

    
    

    $$y''(t)+ 6 y (t)+ 9 y(t) = 6 e^{-3 t}, y(0)=-1, y'(0)=6.$$
    
    

50. Solve Initial Value Problem

    
    

    $$y''(t) + 4 y'(t) + 8y(t) =0, y[0]=1,y'[0]=0.$$
    
    

51. Solve

    
    

    $$t^2 y''(t) - 2 y (t) = 3 t^2 -1, t>0.$$
    
    

52. Find the general solution of the equation
    

    $$x^2y''-xy' +y = 0.$$
    
    

53. Find the general solution of the equation $\quad \displaystyle x^2 y'' -2 x y' + 2 y = \frac{x^3}{1+x^2}.$

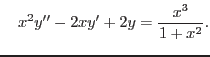
54. Solve the following inhomogeneous ordinary differential equation of a second order
    

    $$x y''(x) - (1+x)y'(x)+y(x) = x^2 e^{2 x}, x>0.$$
    
    

    Note that the general solution to the corresponding homogeneous equation
    

    $$x y_0''(x) - (1+x)y_0'(x)+y_0(x) = 0, x>0.$$
    
    
    is given by
    
    $$y_0(x) = C_1 (1+x) + C_2 e^x.$$
    
    

55. Find the general solution of the equation
    
    $$\quad \displaystyle x^2 y'' -2 x y' + 2 y =1.$$
    
    

56. 2. Find the general solution of the equation
    
    $$\quad \displaystyle x^2 y'' -2 x y' + 2 y =x.$$
    
    

57. Calculate the general solution of the equation
    

    $$(1-x)y^{\prime\prime} + xy^{\prime} -y = (1-x)^{2},$$
    
    
    if the general solution of the corresponding homogeneous equation equals
    
    $$y_{\rm homogeneous}=c_1 x + c_2 e^x.$$
    
    

58. Find the general solution of the differential equation
    
    $$x^2y'' - 4 x y' +6y=x^4\sin x.$$
    
    

59. We have studied in class the equation
    

    $$y'(x)+ p(x) y(x) = g(x),$$ (11)

    
    
    and we have learned the concept of integrating factor. If you multiply both sides of this equation by $e^{\int p(x) d x}$, then it can be represented as
    
    $$(y(x)e^{\int p(x) d x})' = g(x) e^{\int p(x) d x}.$$
    
    
    Then $y(x)$ may be calculated by integrating both sides with respect to $x$.

    Show how to solve equation (11) by method of variation of a parameter. To do this, complete the following steps:

    1. Solve the homogeneous version of the equation (11):
       

       $$y_0'(x)+ p(x) y_0(x) = 0,$$ (12)

       
       
       by separation of variables.
    2. Look for a solution of (11) in a form
       

       $$y(x) = u(x) y_0(x),$$ (13)

       
       
       where $y_0(x)$ is a solution to (12) and $u(x)$ is a function to be found. In other words, substitute (13) into (11) and find equation for function $u(x)$.
    3. Solve the equation for $u(x)$, and write the solution to equation (11).
    4. Compare this answer to solution of equation (11) obtained by integrating factor and comment on the similarities and differences of the integrating factor and variation of a parameter method for solving equation (11).

60. A spring/mass system is modeled by the initial value problem:
    

    $$2u^{\prime\prime} + \gamma u^{\prime} + 8u =0$$
    
    
    
    
    $$u(0) = 1, u^{\prime}(0) = 4.$$
    
    

    (a) Give a qualitatively accurate sketch of $u(t)$ for each indicated value of $\gamma$:
    

    $$\gamma = 4, \quad \gamma = 7.9, \quad \gamma = 10, \quad \gamma = 1000.$$
    
    
    (b) Find the value of $\gamma$ that makes the quasi-period $T_d$ 50% greater than the natural period.

    (c) Extra Credit 5 percent Give a qualitatively accurate sketch of $u(t)$ for
    

    $$\gamma=-4$$
    
    
    and
    
    $$\gamma=-10$$
    
    
    .

61. If an undamped spring-mass system with the mass that weights 6 lb and a spring constant 1 lb/inch is suddenly set in motion from a rest position at an equilibrium at $t=0$ by an external force of $4 \cos 7 t$ lb, determine the position of the mass at any time and scetch a graph of the displacement versus time.

62. A vibrating spring-mass system has mass $m=1$, damping coefficient $\gamma=2$, and spring stiffness $k=2$. At time $t=0$, when the mass is at rest, the force $10\sin 2t$ starts acting on it. What is the motion for all subsequent times, $t$? What motion does the system settle into for large $t$? Does this large-time motion depend on the initial conditions? Sketch this large-time motion.

63. Consider the equation for the Damped Harmonic Oscillator:
    

    $$\ddot x(t) + 2 \beta \dot x(t) + \omega_0^2 x(t)=0.$$
    
    
    1. Choose $\beta$ and $\omega_0$ such that the resulting oscillator is under damped. Sketch $x(t)$. (You do not need to sole for $x(t)$).
    2. Choose $\beta$ and $\omega_0$ such that the resulting oscillator is critically damped. Sketch $x(t)$. (You do not need to sole for $x(t)$).
    3. Choose $\beta$ and $\omega_0$ such that the resulting oscillator is under damped. Sketch $x(t)$. (You do not need to sole for $x(t)$).

64. (a) Some damped vibrating system is described by the equation
    

    $$\ddot{u} + 4 \dot{u} + 5u =0.$$
    
    
    If the initial position is equal to 1 and the initial velocity of this system is equal to $0$, describe the motion of the system for all subsequent times by finding the appropriate solution of this initial-value problem. Express this solution in the form $u=Ae^{-\beta t}\cos(\mu t-\delta)$ for some suitable constants $A$, $\beta$, $\mu$, and $\delta$.

    
    

    (b) If the equation from 2(a) is forced so that it becomes
    

    $$\ddot{u} + 4 \dot{u} + 5u = 2\sin t,$$
    
    
    then one part of its solution, called the stationary state, is dominant for large $t$. Calculate this stationary solution!

65. (a) A vibrating mass-spring system is described by the equation
    

    $$\ddot u+2\dot u+2u=0,$$
    
    
    If, at time $t=0$, the mass is released from the position $u=1$ with no velocity, find the subsequent motion of this system.

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

    (b) Suppose that the vibrating system of part (a) is forced so that
    

    $$\ddot u+2\dot u+2u=\sin t.$$
    
    
    If the system is released from the equilibrium at $t=0$, find what motion the system settles into for large $t$?

66. Some forced mass-spring system is described by the equation
    

    $$\ddot u + 2\dot u + k u = \cos t.$$ (14)

    
    

    (i) For $k>1$, find the solution of (14) that satisfies the initial conditions $u(0)=0$, $\dot u(0)=0$.

    (ii) After an initial transient period, every solution of (14) settles into a stable periodic motion. Identify this motion, and compute its amplitude, A. For what $k$ is $A$ the largest?

    (iii) Roughly sketch the solution $u(t)$ that you have obtained in (i) if you assume that $k\gg 1$.

67. Find the solution of the initial value problem
    

    $$u''(t)+u(t)=F(t), u(0)=0, u'(0)=0,$$
    
    
    where
    
    $$F(t)=\left[\begin{array}{c} F_0 t, 0\le t\le \pi... ...2\pi\\ 0, t> 2\pi. \end{array}\right.$$
    
    

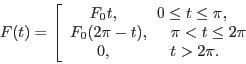
    Treat each time interval separately and match the solutions in the different intervals requiring $u$ and $u'$ are continuous functions of time.

68. A spring mass system has a spring constant of 3 Newtons per meter. A mass of 2 kg is attached to the spring, and the motion takes place in a viscous fluid that offers a resistance numerically equal to the magnitude of the instantaneous velocity (i.e. $\gamma=1 \frac{\rm kg}{\rm sec}$). If the system is driven by an external force of $(3 \cos (3 t) - 2 \sin (3 t)) N$, ¹ determine the steady state response of the system (i.e. the form of the solution when $t\to\infty$). Express your answer as in the form $R\cos (\omega t - \sigma)$. Time is measured in seconds.

69. Some differential equation $y''+p(x)y'+q(x)y=0$ has two linearly independent solutions $y_1(x)=x$ and $y_2(x)=x\ln x$. What is the general solution of the equation
    

    $$y''+p(x)y'+q(x)y=\frac{1}{x}?$$
    
    

70. Let the function $f(x)$ be given in the interval $0<x<\pi$ by the formulas
    

    $$f(x)=\left\{\begin{array}{ll} x, & 0<x<\frac{\pi}{2}, 1, & \frac{\pi}{2}<x<\pi.\end{array}\right.$$
    
    
    Sketch the odd extension of this function with period $2\pi$, and compute the general formula for the coefficients in its Fourier series. Also, evaluate explicitly the first three nonzero coefficients in this series.

71. Find the Full Fourier Series of a Function $f(x)$, defined for $-\pi<x<\pi$ as
    

    $$f(x)= \left\{\begin{array}{ll} 1, & -\pi<x<0, 1-x, & 0<x<\pi.\end{array}\right.$$
    
    

    Calculate explicitly coefficients for $n=0$, $n=1$ and $n=2$.

    Sketch the graph of the function to which the series converges for $-4\pi<x<4\pi$.

72. Find the Full Fourier Series of a Function $f(x)$, defined for $-\pi<x<\pi$ as
    

    $$f(x)= \left\{\begin{array}{ll} 1, & -\Pi<x<0, -2, & 0<x<\pi.\end{array}\right.$$
    
    

    Calculate explicitly coefficients for $n=0$, $n=1$ and $n=2$.

    Sketch the graph of the function to which the series converges for $-4\pi<x<4\pi$.

73. Let the function $f(x)$ be given in the interval $0<x<\pi$ by the formulas
    

    $$f(x)=\left\{\begin{array}{ll} x, & 0<x<\frac{\pi}{2}, 1, & \frac{\pi}{2}<x<\pi.\end{array}\right.$$
    
    
    Sketch the odd extension of this function with period $2\pi$, and compute the general formula for the coefficients in its Fourier series. Also, evaluate explicitly the first three nonzero coefficients in this series.

74. (a) Find the Fourier sine and cosine series of the function
    

    $$f(x)=\left\{ \begin{array}{ll} 0, & 0<x<1, \\ 1, & 1<x<3, \end{array}\right.$$
    
    

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

    (b) Sketch the functions to which the two series of part (a) converge. What is the period of those two functions?

75. (a) Find the Fourier sine and cosine series of the function
    

    $$f(x)=\left\{ \begin{array}{ll} 0, & 0<x<3, \\ 1, & 3<x<4, \end{array}\right.$$
    
    

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

    (b) Sketch the functions to which the two series of part (a) converge. What is the period of those two functions? Are these functions even or odd?

    (a) Find the Fourier series of
    

    $$f(x) = \left\{ \begin{array}{cc} 0, & \!-\pi \leq x < -\pi/2,... ...!\pi/2 \leq x < \pi \end{array}\qquad f(x+2\pi) = f(x) \right.$$
    
    

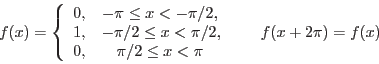
    (b) Sketch the graph of the function to which the series converges for three periods.

76. Find the Fourier Cosine Series for the function $x^4$ for $0< x <1$.

77. Find the Full Fourier Series for the function $x^3$ for $-\pi<x<\pi$ and plot the graph of the function to which the series converge for $-2\pi<x<2\pi.$

78. (a) Find the solution of the eigenvalue problem
    

    $$X''+\lambda X=0,\qquad X(0)=0, \quad X'(\pi)=0.$$
    
    

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

    (b) Find all the solutions $u_n(x,t)$ that satisfy the heat equation
    

    $$u_t=u_{xx},\quad 0<x<\pi,\quad t>0,$$
    
    
    and the boundary conditions
    
    $$u(0,t)=0,\quad u_x(\pi,t)=0,\quad t>0.$$
    
    

79. (a) Find the solution of the eigenvalue problem
    

    $$X''+\lambda X=0,\qquad X(0)=0, \quad X'(1)=0.$$
    
    

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

    (b) Find all the solutions $u_n(x,t)$ that satisfy the heat equation
    

    $$u_t=u_{xx},\quad 0<x<1,\quad t>0,$$
    
    
    and the boundary conditions
    
    $$u(0,t)=0,\quad u_x(1,t)=0,\quad t>0.$$
    
    

80. Find all the eigenvalues and eigenfunctions of the problem
    

    $$X''+\sigma X=0,\qquad X(0)=0,\qquad X'(\pi)=0.$$
    
    

    NOTE: If you use the ``rule of thumb'' mentioned in class, state that explicitly and explain what this rule is.

    NOTE: Consider separately $\sigma>0$, $\sigma=0$ and $\sigma<0$ cases.

    Draw (on the same set of axes) the first three eigenfunctions.

81. Solve
    

    $$y''(x)+4 y(x) = 0,,$$ (15)

    $$y(0) = 0, y'(\pi) = 2.$$ (16)

    
    

    HINT: first solve the ODE (15), its solution has two arbitrary constants. Use boundary conditions (16) to find these two arbitrary constants.

82. Find all the eigenvalues and eigenfunctions of the problem
    

    $$X''+\sigma X=0,\qquad X(0)=0,\qquad X(\pi)=1.$$
    
    

    NOTE: Please consider explicitly positive eigenvalues, zero eigenvalues and negative eigenvalues.

83. Find the solution of the eigenvalue problem
    

    $$X''+\lambda X=0,\qquad X'(0)=0, \quad X'(10)=0.$$
    
    

    NOTE: Please be careful to consider both positive, zero, and negative eigenvalues, or give arguments supporting your choice of sign of the eigenvalues.

84. Find the eigenvalues and eigenfunctions of the problem
    

    $$y''+\lambda y = 0,\qquad y'(0)=0,\quad y(3)=0.$$
    
    
    You may assume that there are no negative eigenvalues.

85. (a) Let $u_{tt}=u_{xx}+9u$. Assuming that $u(x,t)=X(x)T(t)$, find ordinary differential equations satisfied by $X(x)$ and $T(t)$.

    (b) bonus 10 percent Find the steady state of the problem
    

    $$u_{tt}=u_{xx}+9u, \qquad u(0,t)=0,\qquad u_x(2\pi,t)=3.$$
    
    

86. Given that the eigenvalues and eigenfunctions for the problem
    

    $$X''+\lambda X =0,\qquad X'(0)=0, \quad X'(\pi)=0$$
    
    
    are
    
    $$\lambda_n=n^2,\qquad X_n(x)=\cos nx,\qquad n=0,1,2,\ldots,$$
    
    
    use separation of variables to find the functions of $u_n(x,t)$ that satisfy the heat equation
    
    $$u_t=u_{xx},\qquad 0<x<\pi,\quad t>0$$
    
    
    and the boundary conditions
    
    $$u_x(0,t)=0,\quad u_x(\pi,t)=0,\qquad t>0.$$
    
    

87. (a) Let $u_{tt}=u_{xx}+4u$. Assuming that $u(x,t)=X(x)T(t)$, find ordinary differential equations satisfied by $X(x)$ and $T(t)$.

    (b) bonus 10 percent Find the steady state of the problem
    

    $$u_{tt}=u_{xx}+4u, \qquad u(0,t)=0,\qquad u_x(\pi,t)=2.$$
    
    

88. Use separation of variables to find the function $u(x,t)$ that satisfies the heat equation
    
    $$u_t=u_{xx},\qquad 0<x<\pi,\quad t>0$$
    
    
    with the boundary conditions
    
    $$u(0,t)=0,\quad u(\pi,t)=0,\qquad t>0$$
    
    
    and initial condition
    
    $$u(x,t=0) = \sin(x).$$
    
    

    Sketch $u(x,t)$ for three values of $t$.

    NOTE: Please be careful to consider both positive, zero, and negative eigenvalues, or give arguments supporting your choice of sign of the eigenvalues.

89. By using the method of separation of variables replace the partial differential equation
    

    $$\frac{\partial}{\partial t}u(x,t) -x^2 \frac{\partial^2}{\partial x^2}u(x,t) -x \frac{\partial}{\partial x}u(x,t) =0$$ (17)

    
    
    by a pair of ordinary differential equations. Solve these ordinary differential equations. Write down possible solutions of the partial differential equation (17). Do not worry about boundary conditions and initial conditions.

90. Use separation of variables to find the function $u(x,t)$ that satisfies the wave equation
    

    $$u_{tt}=u_{xx},\qquad 0<x<\pi,\quad t>0$$
    
    
    with the boundary conditions
    
    $$u(0,t)=0,\quad u(\pi,t)=0,\qquad t>0$$
    
    
    and initial condition
    
    $$u(x,t=0) = \sin(x), u_t(x,t=0)=0.$$
    
    

    Sketch $u(x,t)$ for three values of $t$.

91. Use separation of variables to replace partial differential equation
    

    $$x^2 u_{xx}+u_{tt}=0,$$ (18)

    
    
    by a pair of ordinary differential equations. Solve these ordinary differential equations. Write down possible solutions of the partial differential equation (19). Do not worry about boundary conditions and initial conditions.

92. Find the general solution of the given system of equations. Sketch a number of representative trajectories.

    $\dot {\mathbf x} = \left(\begin{array}{rr}3 & -2 2 & -2\end{array}\right){\mathbf x}.$

93. Solve by separation of variables the following Partial Differential Equation:

    
    

    $$x^2 \frac{\partial^2}{\partial x^2}u(x,y)+ x \frac{\partial}... ...{\partial y^2}u(x,y)=0, u(x,0)=u(x,\pi)=0, 0<x<2, 0<y<\pi$$ (19)

    
    
    1. if $u(x, y) = X(x)Y (y)$, is a solution to the PDE (19), find two ordinary differential equations satisfied by the functions $X$ and $Y$. Each equation should contain a constant $\lambda$.
    2. Verify that possible solution to your equations are $X (x) = x^m$ and $Y(k) = sin(k y)$, provided that $k$ and $m$ are related to $\lambda$ in a certain way. Find this relation.
    3. Now assume $u(x, 0) = 0$ and $u(x, \pi)$ = 0. What are the allowed values of $k$?
    4. Given the allowed values of $k$, what are the allowed values of $m$?
    5. Write down the resulting solution of this PDE

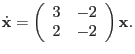
94. (a) Consider the heat conduction problem
    

    $$u_{t}=u_{xx},\qquad 0<x<10,\quad t>0,$$
    
    
    
    
    $$u_{x}(0,t)=10,\qquad t>0,$$
    
    
    
    
    $$u(10,t)=50,\qquad t>0,$$
    
    
    
    
    $$u(x,0)=40-4x,\qquad 0<x<10.$$
    
    
    Find the steady state temperature distribution $v(x)$ that will be approached as $t \rightarrow \infty$.

95. The Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, $\ldots$ is defined by the condition that each successive term is the sum of its two predecessors,
    

    $$a_n=a_{n-1}+a_{n-2}$$ (20)

    
    
    and the two initial terms $a_0=0$, $a_1=1$. Assume a particular solution of the difference equation (20) to be $a_n=\lambda^n$ for some unknown $\lambda$, and compute the two values of $\lambda$ that the equation gives you. By analogy with differential equations, construct the general solution of (20). Then, taking the two initial terms into account, compute the value of the general term $a_n$ of the Fibonacci sequence.