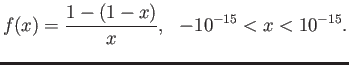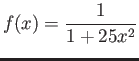- Lectures One, Two, Three: Chapter ONE Introduction
to numerical computing and floating point numbers. Machine
precision, overflow, underflow, normalized numbers and subnormal and
the
 command. Crazy graph of
command. Crazy graph of
J26: errors, decimals and binaries,
- Lectures Four,Five, Six Chapter TWO - finding roots
of nonlinear equations. Bisection, Newton, Secant and Halley methods.
Rate of convergence and fzero command. Chapter Three Solving
.
Forward and Backward substitutions.
- Lecture 8 The Midterm
- Lecture 9-11 Chapter Three Solving the
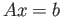 ,
Gauss elimination and
,
Gauss elimination and 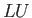 decomposition. Vector and Matrix norms,
properties of norms. Condition number of a matrix. Error estimates.
Residuals. Solving nonlinear system of equations via Newton iterations. q
decomposition. Vector and Matrix norms,
properties of norms. Condition number of a matrix. Error estimates.
Residuals. Solving nonlinear system of equations via Newton iterations. q
- Chapter 4 Lectures 12,13 - Eigenvalues, eigenvectors, examples,
'eig' operation in Matlab, Power iterations, Theorem 4.1 and 4.2
- Lecture 14, inverse Power iterations, power iterations with the
shift.
- Chapter 5 Lectures 15-17, Interpolation. Monomial,
Lagrange, piece-wise linear. Example of
interpolating
, for
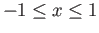 . Wiggles. Cubic Splines. Very boring actual calculation of a cubic spline. Theorems 5.1-5.6
. Wiggles. Cubic Splines. Very boring actual calculation of a cubic spline. Theorems 5.1-5.6
- Chapter 6 Lectures 18-22. Numerical Integration: Left sided,
Mid Point, trapezoid, Simpson, Gaussian, Adaptive. Special
attention to error terms. First lecture: Intro into integration,
and numerical integration of
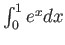 by Left-sided,
Midpoint, Trapezoid and Simpson quadratures. Second Lecture: error estimates for Left-Sided, Midpoint and composit Midpoint.
by Left-sided,
Midpoint, Trapezoid and Simpson quadratures. Second Lecture: error estimates for Left-Sided, Midpoint and composit Midpoint.