HW THREE

1. Problem 3.2

   (a) $(1,0)$ with condition number 6.17 in norm 2

   (b) $(1,\frac{1}{2})$ with condition number 10.98 in norm 2

   (c) $(-\frac{1}{2},2)$ with condition number 6.98 in norm 2

   (d) $(0,-1,1)$ with condition number 2 in norm 2

2. Problem 3.10

   (a)

   $$\begin{bmatrix}a-b c / d & b 0 & d \end{bmatrix} \times \begi... ...}1 & 0 c/d & 1 \end{bmatrix} = \begin{bmatrix}a & b c & d \end{bmatrix}.$$

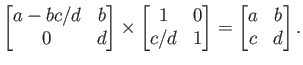
   (b) To solve $A x = b$, write $A=U L$, so that $U L x = b$. Solve by backward $U z = b$, solve by forward $L x = z.$

   (c)

   $$\begin{bmatrix}1 & 0 b/a & 1 \end{bmatrix} \times \begin{bmat... ... 0 & d = b c / a \end{bmatrix} = \begin{bmatrix}a & c b & d \end{bmatrix}.$$

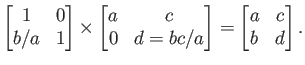
   I do not see obvious connection

   (d)

   The reason we prefer LU to UL is purely conventional, there is no mathematical reason beyound this choice.

3. Problem 3.12

   (a)

   Use page 91 to calculate inverse of a matrix, use 1 norm of the matrix, and assume that $\alpha>0$.

   We get

   $$\vert\vert A\vert\vert _\infty = max(2,\alpha),$$
   and
   $$\vert\vert A^{-1}\vert\vert _\infty = \frac{1+\alpha}{\alpha}.$$

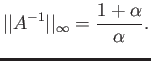
   Then the condition number of a matrix is

   $2 (1+\alpha)/\alpha$ for $0<alpha<2$

   and

   $(1+\alpha)$ for $\alpha>2$.

   Then we conclude that the matrix is ill conditioned for very large and very small values of $\alpha$.

   (b) If the residual is small, but nonzero, the error will be small for small condition number. If condition number is large, the error will be large. So if we take $\alpha\to 0$, the error will be large even for a small residual.

   Use $r = A x' - b$ and $A x = b$, where $x'$ is a numerical solution, to show that $A e = r$. So we have $e = A^{-1} r$ and

   $$\vert\vert e\vert\vert<=\vert\vert A^{-1}\vert\vert \cdot \vert\vert r\vert\vert.$$

   (c) Using $A e = r$ we get $\vert\vert r\vert\vert\le \vert\vert A\vert\vert \cdot \vert\vert e\vert\vert$, so for large $\alpha$ the residual is going to be very large with small error.