Next: Home Work TWO Up: Home work Answers Previous: Home work Answers
a
![]() , where
machine epsilon
, where
machine epsilon
![]() ,
, ![]() is
the base of the system and
is
the base of the system and ![]() is lowest possible value of
exponent.
is lowest possible value of
exponent.
b
![]() with
with
![]() being maximum value of exponent,
being maximum value of exponent,
c
a
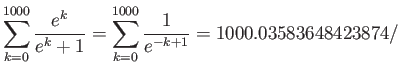
b
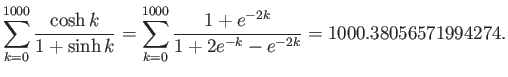
Here we divided numerator and denominator by ![]() to avoid overflow.
to avoid overflow.
c
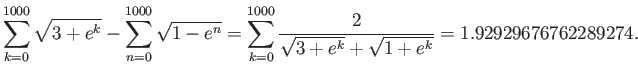
d
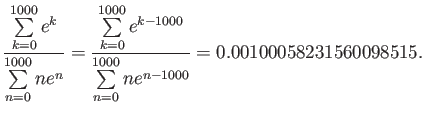
Here we divided numerator and denominator by ![]() to avoid overflow.
to avoid overflow.
e
Calculate
![$\displaystyle X=\sum\limits_{k=1}^{1000}k\left[ \sin\left(\pi(k^{10}+1/k)\right)-
\sin\left(\pi(k^{10}-1/k)\right)
\right].$](img573.png)
Since
![]() , and
, and
![]() ,
and
,
and
![]() , and using the fact that even number raised to the power of 10 is even, and odd number raised to teh power of 10 is odd, we obtain
, and using the fact that even number raised to the power of 10 is even, and odd number raised to teh power of 10 is odd, we obtain
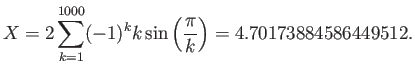
a If Horner right,
b If Horner is right,
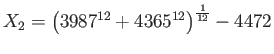
c If Horner is right,
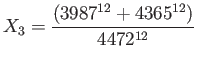
d If Horner is right,
![$\displaystyle X_4=\left[\left(3987^{12}+4365^{12}\right)
^{\frac{1}{12}}\right]^{12} -
4472$](img585.png)
e The product of two ![]() digit numbers may have up to
digit numbers may have up to ![]() digits. Therefore
digits. Therefore ![]() may have up to 48 digits, which is
longer then Matlab's 16 digits. Therefore we can not use doubles in
Matlab to either prove or disprove this conjecture.
may have up to 48 digits, which is
longer then Matlab's 16 digits. Therefore we can not use doubles in
Matlab to either prove or disprove this conjecture.
Note that ![]() can be explicitly calculated on a computer with
inifinite precision (check out vpa command in matlab), because it is
an integer. Using the “sym” command, or Mathematica allows us to
get the answer:
can be explicitly calculated on a computer with
inifinite precision (check out vpa command in matlab), because it is
an integer. Using the “sym” command, or Mathematica allows us to
get the answer:
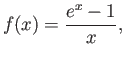
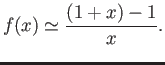
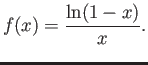
Use Taylor’s theorem to show that
Denoting
b Why
This is due to “rounding to nearest”,c
Since
![]() and
and
![]() , we get
, we get
![]() . More precisely,
. More precisely,
![]() . Use this together with (32) and
(33) to get
. Use this together with (32) and
(33) to get
| (33) |
d This question implies that
To obtain this result, write
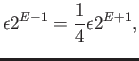
Author's note:
in (d) the right hand side shoule be ![]() and in (e) the right hand side should be
and in (e) the right hand side should be
![]() .
.
e The RHS can be rewritten as
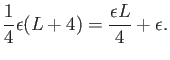
f Using
![]() we get
we get ![]() . Picture
shows that
. Picture
shows that ![]() accuracy is obtained at
accuracy is obtained at ![]() , i.e.
, i.e.
![]() . In other words the estimate is optimistic.
. In other words the estimate is optimistic.