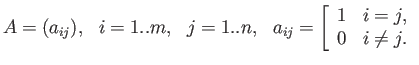- Construct the floating point system where the numbers
may be exactly representable.
- Consider the floating point system with
 digits with base
digits with base 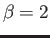 and
lower and upper values of exponents being
and
lower and upper values of exponents being  and
and  .
Subnormals are allowed.
.
Subnormals are allowed.
- How many numbers are there between the number
 and
number
and
number 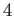 (not counting
(not counting
 and
and 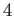 .
.
- What is the number closest to
 ?
?
- What is the smallest INTEGER which is not
representable in this floating point system?
- How would your answer change if
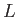 and
and 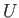 were to be
were to be
 and
and 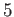 ?
?
- Let
 and
and 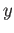 be two adjacent positive Normalized
Single Precision floating point numbers.
be two adjacent positive Normalized
Single Precision floating point numbers.
- What is the minimal possible distance between
 and
and 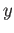 ?
?
- What is the maximum possible distance between
 and
and 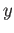 ?
?
- How many Double Precision Numbers are there between
 and
and 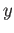 (for double numbers
(for double numbers 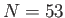 ).
).
- IEEE Single Precision has
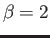 ,
, 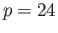 ,
, 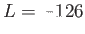 ,
, 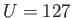 ,
and subnormals are allowed.
What is the maximum integer value of
,
and subnormals are allowed.
What is the maximum integer value of 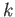 for which the number
for which the number
can be exactly re presentable in Single Precision?
IEEE Single Precision has 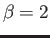 ,
, 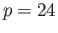 ,
, 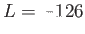 ,
, 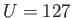 ,
and subnormals are allowed.
,
and subnormals are allowed.
In class we have shown that if  is a real number, and
is a real number, and 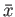 is its
floating point representation, then the maximum possible relative error
in representing this number is given by
is its
floating point representation, then the maximum possible relative error
in representing this number is given by
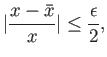 |
(1) |
where 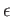 is machine precision,
is machine precision,
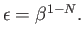
How the equation (1) changes for the subnormals?
To answer this question,
- First, consider
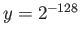 .
How is
.
How is 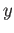 going to be represented in IEEE SP?
going to be represented in IEEE SP?
- What is the floating point number that follows
number
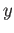 on the computer number line?
on the computer number line?
- What is the maximum possible absolute error
in representing numbers between
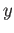 and
and 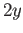 ?
?
- Consider number
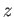 such that
such that
What is
the maximum possible relative error in
representing the number 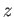 ?
?
- extra credit Generalize the result of the previous
question to any number between
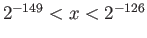 . You
can guess the correct result by contemplating equation
(1).
. You
can guess the correct result by contemplating equation
(1).
- In single precision, what is the floating point number that
follows “32”? In other words, what is the smallest positive
floating point number
 such that
such that
Please write the
result the way it is stored in the computer, i.e. in binary floating
point form.
Consider a floating-point arithmetic with base
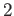 , precision
, precision 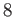 and exponent range
and exponent range ![$ [-16,16]$](img74.png) . In other words, each number in this system
can be represented as
. In other words, each number in this system
can be represented as
Here 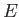 is integer, and all
is integer, and all
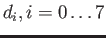 are either 0 or
are either 0 or  .
.
- Show that addition is not necessarily
associative. I.e., give an example of 3 numbers
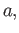
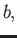 and
and 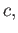 such that
such that
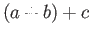 is not equal to
is not equal to 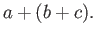
- write down two adjacent normalized numbers
 and
and 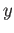 such that
such that 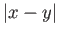 is maximal.
is maximal.
- In this floating point system, what is the range of possible relative errors in representing a given number by a machine number?
(a) Find the largest open interval around 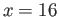 so that all
real numbers from the interval are rounded to
so that all
real numbers from the interval are rounded to 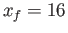 . That is, find
the smallest value of
. That is, find
the smallest value of 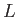 and the largest vlue of
and the largest vlue of 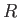 with
with 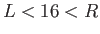 so
that any number from the interval
so
that any number from the interval 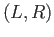 is rounded to the floating
point number
is rounded to the floating
point number 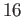 . Assume double precision is used (53 binary digits).
. Assume double precision is used (53 binary digits).
(b)
Redo the part (a) for the 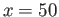 , that is, find the interval
, that is, find the interval 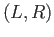 that rounds to the floating point number
that rounds to the floating point number
IEEE SP has 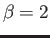 ,
, 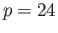 ,
, 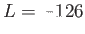 ,
, 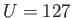 .
.
Calculate  ,
,  and
and
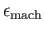 for this system.
Assume rounding by chopping.
for this system.
Assume rounding by chopping.
How many floating point numbers are there between any successive
powers of 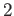 ? For example, how many floating point numbers are there
between 2 and 4?
? For example, how many floating point numbers are there
between 2 and 4?
Consider the floating point system with
(a)
What is the distance from number 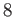 to
the next largest floating point number in this floating point
system?
to
the next largest floating point number in this floating point
system?
(b)
What is the distance from number 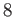 to the next smallest floating point number in this floating point system?
to the next smallest floating point number in this floating point system?
(c) What distance is larger, (a) or (b)? Why? What is the relation between
these distances and machine precision
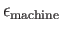 ?
?
- Consider IEEE SP, which has
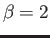 ,
, 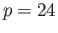 ,
, 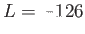 ,
,
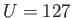 . What is the closest floating point number to
the number
. What is the closest floating point number to
the number
in IEEE SP?
- Consider IEEE SP, which has
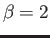 ,
, 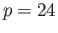 ,
, 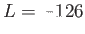 ,
,
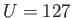 . What is the absolute error in representing
the number
. What is the absolute error in representing
the number
in IEEE SP?
- Consider IEEE SP, which has
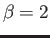 ,
, 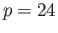 ,
, 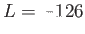 ,
,
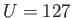 .
What is the closest floating point number to the number
.
What is the closest floating point number to the number
in IEEE SP?
- What is the spacing of the floating point numbers
between
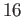 and
and 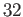 , i.e.
, i.e.
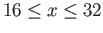 ?
?
- Define machine epsilon and explain its significance
- What would be the output in MATLAB for the ratio
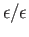 ?
?
- Consider
a) Approximate 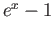 using third degree Taylor polynomial
expanded about
using third degree Taylor polynomial
expanded about 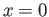 . Use this expansion to show that
. Use this expansion to show that
b) Explain why MATLAB would compute the limit of 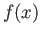 to be 0.
to be 0.
- What is the largest value of
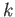 such that
such that
in IEEE SP
system? Here
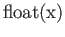 is a floating point
representation of the number
is a floating point
representation of the number  .
.
- We have studied in class that the maximum possible
relative error for normalized numbers is equal to
<
What is the range of possible errors for the subnormal
floating point numbers?
- Consider
function. The following values were obtained in MATLAB:
Please explain in details the values in the right column of
this table.
- For which positive integers
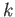 can the number
can the number 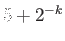 be
represented exactly, with no rounding error in IEEE SP floating
point system?
be
represented exactly, with no rounding error in IEEE SP floating
point system?
Consider IEEE SP that has binary numbers 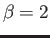 , with
, with  digits, and lower and upper values of the exponents of
digits, and lower and upper values of the exponents of 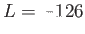 ,
,
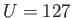 . As we discussed in class, the number
. As we discussed in class, the number
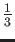 is not
representable in IEEE SP. What is the Floating Point Number that
precedes
is not
representable in IEEE SP. What is the Floating Point Number that
precedes
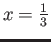 ? In other words, find the largest Floating
Point Number that is less then
? In other words, find the largest Floating
Point Number that is less then
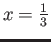 .
.
Hint: your answer should contain 24 binary digits of the
mantissa and the value of the exponent.
- (a)Which of the following operations of two positive floating
point numbers can produce overflow?
— addition
— subtraction
— multiplication
— division
If you answered “yes” to any of the questions, please give one example
of two Single Precision numbers that produce overflow by given operation.
(b) Which of the following operations of two positive floating
point numbers can produce underflow?
— addition
— subtraction
— multiplication
— division
If you answered “yes” to any of the questions, please give one example of two Single Precision numbers that produce
underflow by given operation.
What is the number that follows the number “zero”,
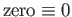 . In other words, find the smallest possible
positive number that is representable in this system. Write the
result in both binary and decimal format.
. In other words, find the smallest possible
positive number that is representable in this system. Write the
result in both binary and decimal format.
Consider the following expression:
assuming
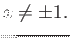
(a) for what values of  it is difficult to calculate this
expresion accurately in floating point arithmetic?
it is difficult to calculate this
expresion accurately in floating point arithmetic?
(b)Give a rearrangement of the terms such that, for the range of  in part
a, the computation is more accurate in floating point system
in part
a, the computation is more accurate in floating point system
- Consider IEEE SP that has binary numbers
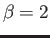 , with
, with  digits, and lower and upper values of the exponents of
digits, and lower and upper values of the exponents of 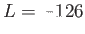 ,
,
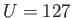 . What is the Floating Point Number that is before
. What is the Floating Point Number that is before 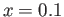 ?
In other words, what is the largest Floating
Point Number that is
less then
?
In other words, what is the largest Floating
Point Number that is
less then 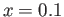 .
.
- Consider the IEEE floating point system, where the binary
numbers
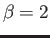 , with
, with  digits, and lower and upper values of
the exponents of
digits, and lower and upper values of
the exponents of 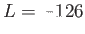 ,
, 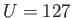 are used. Also, assume that the
“rounding to nearest” rule is used, and if there is a tie, a
smallest number is chosen.
are used. Also, assume that the
“rounding to nearest” rule is used, and if there is a tie, a
smallest number is chosen.
— For what numbers  will the computer claim that inequality
will the computer claim that inequality
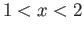 is true?
is true?
— For what real numbers  will a computer claim that
will a computer claim that
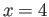 ?
?
— Suppose it is claimed that the solution  of
of 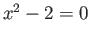 is
exactly representable in this system. Why it is not possible? What
is the distance between two floating point numbers that is right
above and right below solution of
is
exactly representable in this system. Why it is not possible? What
is the distance between two floating point numbers that is right
above and right below solution of 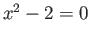 in this system?
in this system?
- Consider the following toy floating point system: base
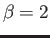 ,
with
,
with 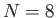 digits, with lower exponent of
digits, with lower exponent of 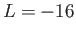 and upper exponent
and upper exponent
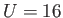 .
.
Consider the following claim: If the two positive binary floating
point numbers  and
and 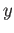 in this toy floating point systems are
such that
in this toy floating point systems are
such that
then their difference, 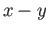 is exactly representable number in the floating
point system.
is exactly representable number in the floating
point system.
Is this claim true or false? If it is true, explain why, if it is
false, find counter example.
-
Consider the following function:
The value of this function for any  is equal to one. However, when
we calculate
is equal to one. However, when
we calculate 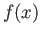 on the computer for small value of
on the computer for small value of  , result is
not equal to
, result is
not equal to  . Here is a computer generated graph of
. Here is a computer generated graph of 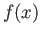 for small value of
for small value of  .
.
Please explain why this graph looks the way it does.
In particular, answer the following questions:
- Why
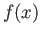 is zero for
is zero for
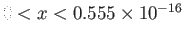 ?
?
- Why
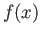 is zero for
is zero for
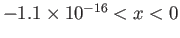 ? Why the value
of zero on the left is twice longer than the value of zero on the
right?
? Why the value
of zero on the left is twice longer than the value of zero on the
right?
- Why after zero,
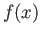 jumps to the value of
jumps to the value of 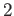 at
at
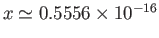 ?
?
- Why does
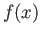 oscillate around
oscillate around 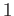 for
for
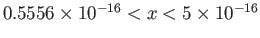 ?
?
- Why does oscillation diminish, as
 become larger
become larger
- Why oscillations are twice as frequent for positive
 than for negative
than for negative  ?
?
- Explain why does the second jump appear at
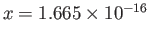 .
.
- Assume a normalized floating point system with base
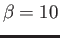 , three digits of accuracy
, three digits of accuracy 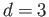 and the lowest possible
exponent of
and the lowest possible
exponent of 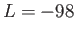 .
.
- What is the smallest possible positive floating point number that
is representable in this system (also called “UFL” for underflow
level)?
- If
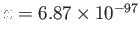 and
and
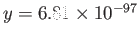 , what is the
result of computing
, what is the
result of computing 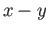 ?
?
- If the subnormal numbers were to be allowed, what would be the
result of
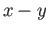 ?
?
IEEE SP has 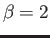 ,
, 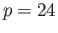 ,
, 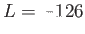 ,
, 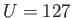 . In single precision
floating point system write down the floating point number that
follows the number
. In single precision
floating point system write down the floating point number that
follows the number 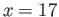 . (In other words, find minimal value of
. (In other words, find minimal value of
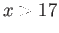 , that is exactly representable in this floating point system.
, that is exactly representable in this floating point system.
IEEE SP has 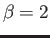 ,
, 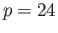 ,
, 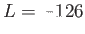 ,
, 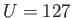 . What is the
smallest possible positive integer that is not a single precision
number?
. What is the
smallest possible positive integer that is not a single precision
number?
- In a floating point system with precision
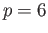 decimal digits,
decimal digits,
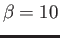 , let
, let 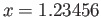 and
and 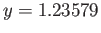 .
.
- How many significant digits does the difference
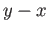 contain?
contain?
- If the floating point system is normalizes, wwhat is hte minimum exponent range for which
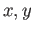 and
and 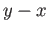 are exactly representable?
are exactly representable?
- Is the fifference
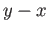 exctly representable, ragardless of
exponent range, if gradual underflow is allowed? Why?
exctly representable, ragardless of
exponent range, if gradual underflow is allowed? Why?
Suppose one calculates using computer arithmetic the following number:
We have shown in class that one can estimate the machine precision by
the number 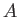 , so that
, so that
Determine whether the following examples may be used to determine
machine precision:
and
Explain your reasoning by using the system with two digits of
precision.
You may find it helpful to use
calculator to gain intuition for this problem.
Consider a floating-point number system with base
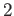 , precision
, precision 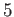 and exponent range
and exponent range ![$ [-10,10].$](img157.png) I.e., in this system
any number can be written as
I.e., in this system
any number can be written as
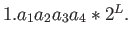
(a) Write down two adjacent normalized numbers  and
and 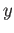 such
that
such
that
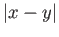 is minimal.
is minimal.
(b) In this floating-point system, what is the maximal possible
error of representing 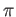 by a machine number? What is the possible
relative error in representing
by a machine number? What is the possible
relative error in representing 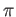 by a machine number?
by a machine number?
(c) In this floating-point system, how many numbers are there
between number 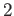 and number
and number 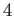 .
.
Assume a decimal (base 10) floating point system having machine
precision
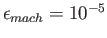 and an exponent range of
and an exponent range of 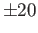 . What is the result of each of the following floating point
arithmetic operations?
. What is the result of each of the following floating point
arithmetic operations?
Chapter TWO
- Suppose you are solving
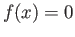 by iterations, and you
have obtained
by iterations, and you
have obtained
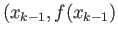 and
and
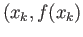 . Now
use linear interpolation to find
. Now
use linear interpolation to find
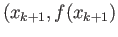 such
that
such
that
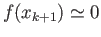 . What is the resulting method of solving
. What is the resulting method of solving
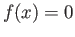 that you have obtained?
that you have obtained?
- For the secant, Newton, and bisection methods: Looking at
iterative error when solving
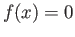 , which of these
methods converges to an error of
, which of these
methods converges to an error of 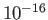 the fastest?
the fastest?
- True or False:
If Newton's method converges to a solution 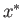 for a particular choice of
for a particular choice of 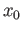 , then it will converge to
, then it will converge to 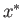 for
any starting point between
for
any starting point between 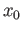 and
and 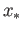 .
.
To get credit for this
problem, you will need to give comprehensive explanation of your
answer.
- For compyting the midpoint
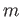 of an interval
of an interval ![$ [a,b]$](img180.png) , which of the following two equations is prefereable in floating point system? Why? When? Devise
the example when the midpoint given be the equation lies outside
of the
, which of the following two equations is prefereable in floating point system? Why? When? Devise
the example when the midpoint given be the equation lies outside
of the ![$ [a,b]$](img180.png) interval.
interval.
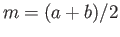 ,
,
-
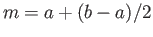 .
.
Solve with three digits accuracy an equation
Note that you have to find two roots. What version of quadratic formulas are you going to
use to find these roots?
- The “divide and average” method for computing a square root
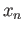 of a given number
of a given number 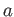 can be formulated
as follows:
can be formulated
as follows:
Show that this method converges to 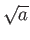 , i.e. that
, i.e. that
and calculate the rate of convergence.
- Show that if
for nonzero 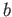 , then the Newton method, converging to the root
, then the Newton method, converging to the root
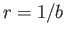 can be implemented without performing any divisions. new
can be implemented without performing any divisions. new
Newton method for solving a scalar nonlinear equation 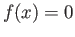 requires computation of the derivative of
requires computation of the derivative of 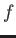 at each
iteration. Suppose that we instead replace the true derivative with a
constant value
at each
iteration. Suppose that we instead replace the true derivative with a
constant value 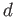 , that is we use the iteration scheme
, that is we use the iteration scheme
(a) Under what condition on value of 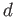 will this scheme be locally
convergent?
will this scheme be locally
convergent?
(b) What is the convergence rate of this scheme?
(c) Is there any value of 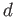 to give a quadratic convergence?
to give a quadratic convergence?
In class we have shown that Newton method
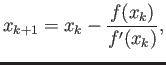 |
(2) |
has quadratic rate of convergence for simple root (i.e. when
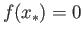 and
and
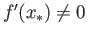 ). In the homework you have shown that
convergence rate is linear for the double root.
). In the homework you have shown that
convergence rate is linear for the double root.
Proove, that Newton method has linear rate of convergence
for triple root, i.e. when
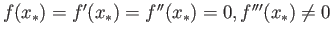 .
.
Extra Credit Proove it for roots of multiplicity 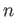 ,
i.e. when
,
i.e. when
- Suppose you came to the Ice Age, and computer in your Time Machine is
broken. Suppose to come back to 2016 to complete the numerical
computing exam, you need to calculate “two to the power one third”, i.e.
. You can only
use 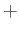 ,
,  ,
, 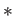 and
and 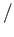 . Set up the nonlinear equation that has
. Set up the nonlinear equation that has
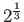 as the solution.
as the solution.
- Describe how to use the bisection method to make this
calculation. What is your initial bracket? How many iteration steps
do you need to perform to get the solution with
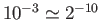 accuracy?
accuracy?
- Describe how to use the Newton method for this calculation. How many
steps do you need to do to get the root with
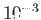 accuracy?
accuracy?
- Consider the following iteraton methods
Assume that all iterations start from 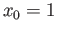 .
.
- 4 points
Verify that each of these fixed-point iterations converge to
![$ \sqrt[3]{21}$](img210.png) , i.e.
, i.e.
and
- rank the methods in order based on their
apparent speed of convergence (i.e. find the fastest method to converge,
the second fastest, the third and the last to converge).
In class we have shown that fixed point iterations
converge if
Under what condition fixed point
iterations converge if
To gain an intuition on this problem, consider the
fixed point iterations
For this problem the fixed point is 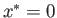 . Start with
. Start with 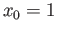 . Then
. Then
It seems to converge to the fixed point 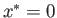 , yet
, yet
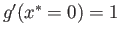 .
Why is that?
.
Why is that?
Consider the function
The graph of the function is given by
As you see from the graph, this function has three roots, given by
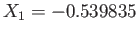 ,
,
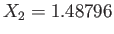 and
and
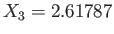 .
.
The following two functions are defined as
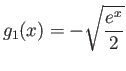 |
|
|
|
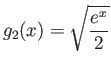 |
|
|
(3) |
Consider the following fixed point iterations:
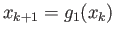 |
|
|
(4) |
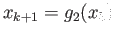 |
|
|
(5) |
- Show that fixed point iterations (4)
with
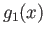 converges to the root
converges to the root 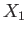 .
.
- Show that fixed point iterations (5) with
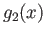 converges to
the root
converges to
the root 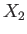 .
.
- Show that iterations with neither
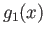 nor
nor 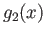 converge to the
root
converge to the
root 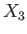 , regardless of the starting point.
, regardless of the starting point.
- Propose a fixed point iteration scheme that will converge to the
root
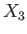 .
.
We have studied Secant method
- Show that it can be equivalently rewritten as
- List two advantages and two disadvantages of Secant method relative
to Newton method.
- Suppose you are solving
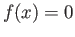 by iterations, and you have
obtained
by iterations, and you have
obtained
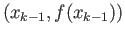 and
and
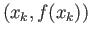 . Now use
linear interpolation to interpolate a straight line through these
two points, and choose
. Now use
linear interpolation to interpolate a straight line through these
two points, and choose 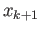 so that
so that
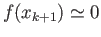 . What is the resulting method of solving
. What is the resulting method of solving 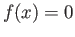 that you
have derived?
that you
have derived?
- Express the Newton iteration method for solving the following
system of nonlinear equations:
and carry out
one iteration starting from the starting point 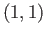 .
.
- Express the Newton iteration method for solving the following
system of nonlinear equations:
and carry out
one iteration starting from the starting point 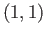 .
.
Carry out one iteration of Newton's method applied to
the system
with starting value
![$ {\bf x}_{0}=[0,1]^{T}.$](img247.png)
The following values for the solution of 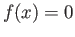 were computed
using Matlab. What method was used (bisection, Newton or secant)? Make sure you explain in details
why it is the method you claim:
were computed
using Matlab. What method was used (bisection, Newton or secant)? Make sure you explain in details
why it is the method you claim:
X=50.25125628140704
X=25.378140640072242
X=12.944094811287638
X=6.7320923307183715
X=3.636103634563207
X=2.1079101939699143
X=1.3816957571715662
X=1.0826201384421688
X=1.0058580941730362
X=1.0000339198559194
X=1.0000000011504786
X=1.0000000000000000
X=1.0000000000000000
Chapter THREE
- Show that for arbitrary square matrices
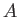 and
and 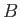 the following
is true
the following
is true
- Show that for arbitrary square matrices
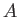 and
and 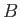 the following
is true
the following
is true
where  denotes the transposition
denotes the transposition
- Prove or give counterexample: if
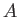 is a singular matrix, then
is a singular matrix, then
- Consider the following systems of equations:
or
- Sketch the two curves and explain where approximately the solutions are located
- Set up and explain the Newton method to find the
solutions. Calculate the Jacobian
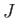 and the RHS
and the RHS 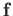 of the
Newton method.
of the
Newton method.
- What would be the good starting point for your calculations?
- Write down in all details the system of equations to make the
first iteration. Do not solve the resulting equations.
-
Suppose that you use Newton method
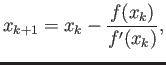 |
(6) |
to find the solution of the equation
for which
What would be the convergence rate for the Newton method for such a case?
HINT: convergence of the Newton method is not necessarily quadratic.
- (a)
Let
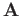 be an arbitrary square matrix, and let
be an arbitrary square matrix, and let 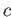 be an arbitrary
scalar.
be an arbitrary
scalar.
Prove or disprove the following statements:
(i)
(ii)
(b)
Let 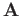 be an
be an 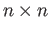 diagonal matrix with
all its diagonal entries equal to
diagonal matrix with
all its diagonal entries equal to 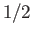 .
.
(i) What is the value of
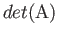 ?
?
(ii) What is the value of
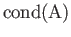 ?
?
Consider the linear system
- Solve this system by any method you like using exact arithmetic.
- Solve this system by computing an inverse of
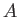 using two
decimal digit machine arithmetic.
using two
decimal digit machine arithmetic.
Hint
If
then
Also
- Now solve (9) by using LU factorization
using two
decimal digit machine arithmetic.
- Compare and explain the difference between results obtained in
items 1, 2 and 3. What conclusion can you make about LU factorization and
computing solution of (9) by using inverse of a matrix?
In this problem
(a) Find a vector  such that
such that
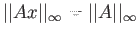 .
.
(b) Find a vector  such that
such that
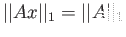
- Consider the
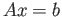 problem with
problem with 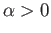 and
and
Suppose that the error
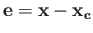 in
computed solution is small, but nonzero. Here
in
computed solution is small, but nonzero. Here 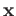 is an exact
solution, and
is an exact
solution, and 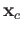 is a computed solution. For what values of
is a computed solution. For what values of
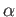 , if any, the residual will be large?
, if any, the residual will be large?
HINT For what values of 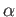 , if any, the matrix
, if any, the matrix 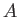 will be
ill-conditioned?
will be
ill-conditioned?
HINT
If
then
The Kronecker delta (named after Leopold Kronecker) is a function of
two variables, usually two integers, is defined as
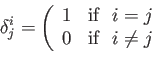 |
|
|
(7) |
Consider the  matrix
matrix  defined as
defined as
In other words, 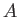 is a diagonal matrix with diagonal entries being equal to
is a diagonal matrix with diagonal entries being equal to
- What is the one norm of this matix?
- What is the two norm of this matrix?
- What is the
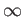 norm of this matrix?
norm of this matrix?
- What is the Condition Number of this matrix?
For the matrix
find the 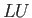 -factorization (show both
-factorization (show both 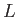 and
and 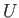 matrices explicitly).
matrices explicitly).
- Consider the system
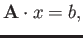 |
(8) |
where
and
or
and
(a) Find explicitly 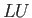 factorization of
factorization of 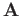 .
.
(b) Use this 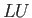 decomposition to solve (9).
decomposition to solve (9).
- Consider the matrix
Calculate the inverse of this matrix  by representing the matrix as a
product of two elementary Gauss elimination matrices.
by representing the matrix as a
product of two elementary Gauss elimination matrices.
- In this problem
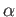 is a small positive number. Sketch the
two lines in the
is a small positive number. Sketch the
two lines in the 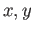 plane, and describe how they change,
including the point of intersection, as
plane, and describe how they change,
including the point of intersection, as 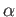 approaches
zero. Also, calculate the condition number for the matrix, and
describe how it changes, when
approaches
zero. Also, calculate the condition number for the matrix, and
describe how it changes, when 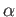 approaches zero.
approaches zero.
- Prove that the one norm is the maximum absolute column sum; use
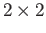 matrices.
matrices.
- Consider
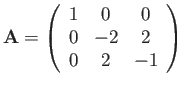 |
|
|
(9) |
a) Find the LU factorization of the given matrix
b) Calculate the norms 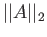 ,
,
 , and
, and  for
this matrix
for
this matrix
c) Calculate the condition number for the matrix A.
- Consider
- Find all vectors satisfying
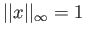 and
and
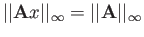 .
.
- Find a vector satisfying
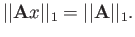
- Find a vector satisfying
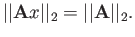
- The
 norm of a vector is defined as a modulus of a maximum
component of a vector. As we learned in class, matrix norms are
defined through the vector norms as
norm of a vector is defined as a modulus of a maximum
component of a vector. As we learned in class, matrix norms are
defined through the vector norms as
Use this definition of the matrix  norm through the
vector norm to proove that the
norm through the
vector norm to proove that the  norm of a matrix is a
maximum absolute row sum.
norm of a matrix is a
maximum absolute row sum.
Complete the proof for 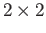 matrices.
matrices.
b
Extra credit 10% Prove this statement for general  matrices.
matrices.
- Consider the system
![\begin{displaymath}\left[
\begin{array}{ll}
4 & 2 \\
2+\varepsilon & 1+\varepsi...
...y}\right] =\left[
\begin{array}{l}
2 \\
1
\end{array}\right]
.\end{displaymath}](img294.png) |
|
|
(10) |
where
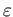 is small. The system has two approximate
solutions
is small. The system has two approximate
solutions
![$ {\bf\hat{x}=}[0,1]^{T}$](img296.png) and
and
![$ {\bf\tilde{x}=}[1-5\varepsilon ,-1]^{T}.$](img297.png) Find the norms of the respective
residuals. Which one is smaller? Find the condition number of the
matrix. Explain, why you should not use residuals in this case to
determine the quality of a solution.
Find the norms of the respective
residuals. Which one is smaller? Find the condition number of the
matrix. Explain, why you should not use residuals in this case to
determine the quality of a solution.
Hint: Find an exact
solution to (11).
Hint
- Calculate an inverse of the following matrix:
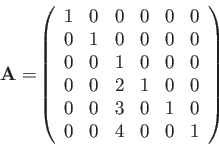 |
|
|
(11) |
Calculate the inverse of this matrix,
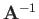 .
.
- Let a
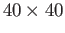 matrix
matrix 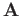 be factored as
follows:
be factored as
follows:
 |
|
|
(12) |
where the blank spaces stand for zeros. Use the LU factorization to solve the system
![$ {\bf Ax=[}0,1,-1,1,...,-1,1]^{T}.$](img303.png)
- Consider the matrix
- What is the determinant of
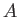 ?
?
- In floating point arithmetic, for what range of
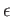 will the
computed value of the determinant be nonzero
will the
computed value of the determinant be nonzero
- What is the
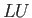 factorization of
factorization of 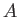 ?
?
- In floating point arithmetic, for what value of
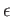 will the
computed value of
will the
computed value of 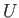 be singular?
be singular?
- In a computer with no build in function for floating point divisions,
one might instead use multiplication by the reciprocal of the divisor.
Apply Newton's method to produce an iterative scheme to approximate the
reciprocal of a number
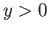 , to solve the equation
, to solve the equation
given y. Considering intended application your scheme should not contain any
divisions.
- Consider the following system of equations:
- Sketch the two curves and explain where approximately the solutions are located
- Set up and explain the Newton method to find the
solutions. Calculate the Jacobian
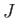 and the RHS
and the RHS 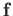 of the
Newton method.
of the
Newton method.
- What would be the good starting point for your calculations?
- Write down in all details the system of equations to make the
first iteration. Do not solve the resulting equations.
- Let a
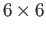 matrix
matrix 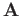 be factored as
follows:
be factored as
follows:
Using this factorization, solve for  the following equation:
the following equation:
Chapter FOUR
The Kronecker delta (named after Leopold Kronecker) is a function of
two variables, usually two integers, is defined as
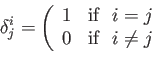 |
|
|
(13) |
Consider the 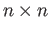 matrix
matrix 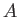 defined as
defined as
In other words, 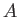 is a diagonal matrix with diagonal entries being equal to
is a diagonal matrix with diagonal entries being equal to
- Find eigenvalues of
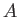 .
.
- Find eigenvectors of
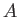 .
.
- To which eigenvector would a power iteractions converge?
Explain, how to set up such power iterations.
- To which eigenvector would an inverse power iteraction converge?
Explain, how to set up such power iterations.
- What algorithm would you use to find second largest eigenvector
and corresponding eigenvalue? Please explain in details.
- Let the
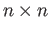 matrix
matrix 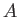 have eigenvalues
have eigenvalues
 , and eigenvectors
, and eigenvectors
 . Let the
. Let the
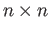 matrix
matrix 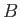 have eigenvalues
have eigenvalues
 and same
eigenvectors
and same
eigenvectors
 . What are eigenvectors and eigenvalues
of the matrix
. What are eigenvectors and eigenvalues
of the matrix  given by
given by
-
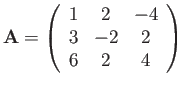 |
|
|
(14) |
a) Calculate the Eigenvalues and Eigenvectors for the given matrix
b) What Eigenvalue would the inverse power method converge to? Why?
c) What Eigenvalue would the power method converge to? Why?
d) Define
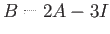 . For this matrix, what Eigenvalue would the
power method converge to? Why?
. For this matrix, what Eigenvalue would the
power method converge to? Why?
Consider the 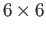 matrix
matrix
- Find Eigenvalues and Eigenvectors of this matrix
- Find LU decomposition of this matrix
- To what eigenvalue and eigenvector the power iteration
will converge?
- To what eigenvalue and eigenvector the inverse power iteration
will converge?
Suppose that 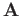 is a symmetric
is a symmetric 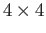 matrix with
eigenvalues
matrix with
eigenvalues
a) To which of these eigenvalues will the power method converge? Why
b) To which of these eigenvalues will the inverse power iteration
converge? Why?
c) To what eigenvalue the power iteration method applied to the matrix
will converge? Why?
Consider
(a) Find eigenvalues and eigenvectors of 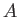 .
.
(b) Find eigenvalues and eigenvectors of
Note that you do not have to calculate 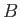 explicitly.
explicitly.
Chapter FIVE
- Given
on the interval
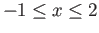 , use the points
, use the points
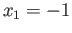 ,
, 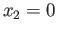 and
and 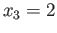 .
.
a) Find the piecewise linear interpolation function
b) find the quadratic interpolation function
- Consider
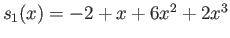 for
for
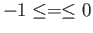
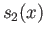 for
for
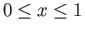 .
.
Solve for 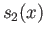 so that the given function is a natural cubic
spline from
so that the given function is a natural cubic
spline from
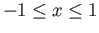 .
.
- Use the theorems we studied in class to calculate the maximum error
in interpolating the function
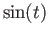 by a polynomial of degree four
using five equally spaced points on the interval
by a polynomial of degree four
using five equally spaced points on the interval ![$ [0,2\pi]$](img330.png) .
.
- Suppose you want to interpolate the function
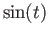 by a
polynomial of degree
by a
polynomial of degree 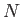 by using
by using 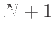 equally spaced points on the
interval
equally spaced points on the
interval ![$ [0,2\pi]$](img330.png) . How many points should you use so that the
difference between the sine function and your interpolation is less
that
. How many points should you use so that the
difference between the sine function and your interpolation is less
that 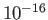 ?
?
- For a set of
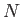 given data points
given data points
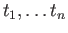 , define the function
, define the function
- Show that
- Show that the
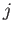 'th Lagrange basis function can be expressed as
'th Lagrange basis function can be expressed as
- In general, is it possible to interpolate
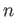 data points by a piecewise
quadratic polynomial, with knots at a given data points, such that the
interpolant is
data points by a piecewise
quadratic polynomial, with knots at a given data points, such that the
interpolant is
- once continuously differentiable?
- twice continiously differentiable
Explain your answer as best as you can.
- What is the maximum number of points
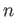 that can be interpolated by
a piecewise quadratic polynomial that is twice continuously
differentiable?
that can be interpolated by
a piecewise quadratic polynomial that is twice continuously
differentiable?
Consider the following data
- Interpolate this data by a quadratic polynomial by using monomial
interpolation
- Interpolate this data by using Lagrange interpolation
- Show that Lagrange interpolation reduces to monomial interpolation
- The Gamma function
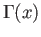 has the following known values:
has the following known values:
Use quadratic interpolation to determine the value
approximate value of  such that
such that
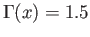 .
HINT: Instead of using the data
.
HINT: Instead of using the data
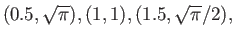 you may find it easier to use the data
you may find it easier to use the data
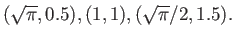
Suppose that some measurements had produced the
following data:
(i)
Write down second degree polynomial passing through all three points
by using Lagrange interpolation
(ii)
Write down second degree polynomial passing through all three
points by using Newton interpolation
(iii)
Show that the two polynomials obtained in (i) and (ii) are equivalent
Use appropriate Lagrange interpolating
polynomial of to interpolate the following data:
What is the degree of
interpolating polynomial? There is a catch in this question.
Consider the following data:
- Interpolate this data by a quadratic polynomial by using monomial
interpolation
- Interpolate this data by using Lagrange interpolation
- Show that Lagrange interpolation reduces to monomial interpolation
- Interpolate this data by piece wise linear interpolation
Determine the parabola (interpolating polynomial of
degree two) that interpolates the values of  for
for
- Find the clamped cubic spline
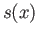 , which goes through the
points
, which goes through the
points
with the value of the first derivative being equal to
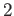 and
and 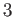 at the beginning and the end of the domain, i.e.
at the beginning and the end of the domain, i.e.
- Find the clamped cubic spline
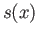 , which goes through the
points
, which goes through the
points
with the value of the first derivative being equal to
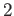 and
and 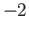 at the beginning and the end of the domain, i.e.
at the beginning and the end of the domain, i.e.
Consider the following function
Is 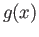 a cubic spline for
a cubic spline for
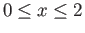 ? Make sure you justify your answer
? Make sure you justify your answer
- Consider the logarithmic function
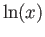 evaluated at the points
1,2 and 3:
evaluated at the points
1,2 and 3:
Write down the entries of the matrix and right hand side of the
linear system that determines the coefficients for the cubic
not-a-knot spline (variation: natural) interpolating these three points.
HINT: not-a-knot spline requires that the third derivative is
continuous at the first and last points.
Do not solve this system.
- Suppose you were to define a piece-wise quadratic spline that
interpolates
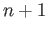 given values
given values
Write down in general form 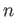 quadratic polynomials that
interpolate these
quadratic polynomials that
interpolate these 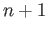 points, such that the resulting piece wise
quadratic polynomial has continuous first derivative. How many
additional conditions are required to make a square system for the
coefficients of this quadratic spline?
points, such that the resulting piece wise
quadratic polynomial has continuous first derivative. How many
additional conditions are required to make a square system for the
coefficients of this quadratic spline?
- This problem considers the function
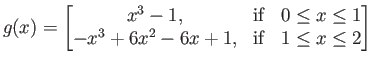 |
|
|
(15) |
- Is
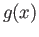 a cubic spline for
a cubic spline for
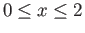 ?
?
- If it is a spline, it is natural, clamped, or neither?
Make sure to justify your answers.
- This problem considers the function
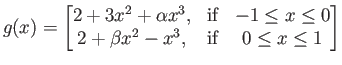 |
|
|
(16) |
- For what values of
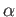 and
and 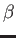 , if any, is
, if any, is 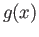 a cubil spline for
a cubil spline for
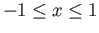 ? These values are to be used for the rest of this problem.
? These values are to be used for the rest of this problem.
- What were the data points that give rise to this cubic spline?
- for what values of
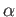 and
and 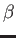 is
is 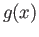 a natural cubic
spline?
a natural cubic
spline?
- for what values of
 and
and 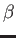 is
is 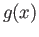 a clamped cubic
spine?
a clamped cubic
spine?
Suppose you are given 4 point:
- Is it possible to interpolate these points by
piece-wise cubic polynomial with
continuous first,second and third derivatives?
- Is it possible to interpolate these points by
piece-wise cubic polynomial with
continuous first,second, third and fourth derivatives?
Please explain your reasoning as accurately as you can.
a
Suppose that you would like to obtain a quadratic spline that
interpolates the function 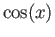 between the nodes 0,
between the nodes 0,  and
and 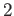 .
.
- Write down the form of the spline interpolation function. How many
coefficients need to be determined?
- Write down the conditions that the spline must satisfy, and the
corresponding equations for the coefficients. Do not solve the
resulting equations.
- Are there enough conditions? If not, what extra condition(s)
would you recommend to make a best possible fit of
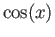 ?
?
b Given a function on a discrete set of 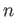 data points. Explain the
difference between interpolation and approximation. What Is the difference
between an interpolating polynomial of degree
data points. Explain the
difference between interpolation and approximation. What Is the difference
between an interpolating polynomial of degree 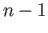 and an approximating
polynomial of the same degree
and an approximating
polynomial of the same degree 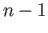 ?
?
Is it possible to interpolate three points
by a second order piece wise continious quadratic polynomial with
continious first and second derivatives?
Is it possible to interpolate four points
by a second order piece wise continious quadratic polynomial with
continious first and second derivatives?
Suppose that you would like to obtain a quadratic spline that
interpolates the function 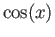 between the nodes
between the nodes ![$ [0,1,2]$](img370.png) .
.
- Write down the form of the spline interpolation function. How many
coefficients need to be determined?
- Write down the conditions that the spline must satisfy, and the
corresponding equations for the coefficients. Do not solve the
resulting equations.
- Are there enough conditions? If not, what extra condition(s)
would you recommend?
Suppose that you are given 4 experimental points:
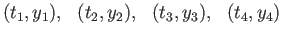 .
.
Is it possible to interpolate these 4 data points by piecewise quadratic polynomial with knots at these given data points, such that
interpolant is
- Once continuously differentialble?
- Twice continuously differentialble?
- Three times continuously differentialble?
In each case, if the answer is “yes” explain why, and outline the
procedure to find the interpolating function (you may use short form of
the equations, do not solve the
resulting equations); if the answer is “no”, explain why.
- In class we have studied cubic splines, i.e. interpolation by a
piece wise cubic polynomial with continious first and second
derivative. It is possible to also introduce quadratic spline,
i.e. piece wise quadratic polynomial with continious first
derivative. Such qudratic spline is the focus of this problem.q
Consider the same data:
Interpolate this data by piece wise quadratic polynomial with
continious first and second derivative at a middle point.
Extra Credit, 30 percent Suppose that one additional point is
added to the above data, so that there are four points.
Is it possible to interpolate this data by piece wise quadratic
interpolation with continious first and second derivatives at the
interior points? Is it possible to do it in general?
Chapter SIX
- In class we have studied quadrature rules of the form
It appears that sometimes it is advantageous to derive quadratures
which also use the derivatives of the function, in addition to value
of the function at selected points. Find the weights for the
quadrature
Chose the weights
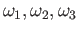 to maximize the precision of the quadrature. What is the
order of the resulting quadrature?
to maximize the precision of the quadrature. What is the
order of the resulting quadrature?
Derive the error term of this quadrature.
In class we have studied quadrature rules of the form
It appears that sometimes it is advantageous to derive quadratures
which also use the derivatives of the function, in addition to value
of the function at selected points. Find the weights for the
quadrature
Chose the weights
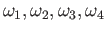 to maximize the precision of
the quadrature. What is the order of the resulting quadrature?
to maximize the precision of
the quadrature. What is the order of the resulting quadrature?
HINT Solution of this problem will be much easier if you guess
the relationship between 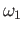 ,
, 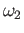 ,
, 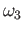 and
and
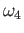 .
.
Derive the error term of this quadrature.
Consider the qudrature rule of the form
Choose 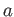 and
and 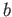 to maximize the accuracy of the resulting
quadrature. Calculate the truncation error of the resulting
quadrature.
to maximize the accuracy of the resulting
quadrature. Calculate the truncation error of the resulting
quadrature.
Is it more accurate or less accurate than Midpoint
quadrature?
Given the points
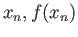 :
:
a) Evaluate the integral of the function using the midpoint rule
b) Evaluate the integral using Simpson's rule
c) Evaluate the integral using the trapezoid rule
(a) Consider the integration rule of the form
Choose 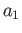 and
and 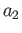 to maximise the precision of this quadrature
rule 16 points
to maximise the precision of this quadrature
rule 16 points
(b) Calculate truncation error of this quadrature.
This problem concerns using numerical methods to calculate the integral
Note that the exact value is
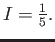
We are going to compare different ways to calculate this integral by
using the value of the function
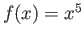 on only three points,
on only three points,
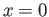 ,
,
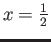 and
and 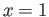 .
.
- Using the composite trapezoidal rule, and 2 subintervals, find an
approximate value for the integral. What is the error?
- Using the Simpson rule on an
![$ [0:1]$](img393.png) interval find the
approximate value of this integral. What is the error?
interval find the
approximate value of this integral. What is the error?
- out of two methods used above, which one gives more accurate
answer, and why? Make sure you justify your answer.
- Extra Credit 10 percent Do the errors you obtained with
Simpson and composite trapezoid above agree with the predictions
given by the theorems we studied in class?
- Let us denote
As you know, we can calculate the value of this integral analytically:
Calculate the value of this integral numerically by using
- Modpoint method
- Trapezoid method
- Simpson method
- Two point Gauss quadrature
Compare the result of your calculations with the exact value. Which of
these four methods give the most accurate result? Is this consistent with
your expectations?
(a) Consider the integration rule of the form
Choose  and
and 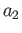 to maximise the precision of this quadrature
rule 16 points
to maximise the precision of this quadrature
rule 16 points
(b) Calculate truncation error of this quadrature.
Find 3-point Gaussian rule for
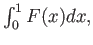 if the standard 3-point Gaussian rule is given by
if the standard 3-point Gaussian rule is given by
(b) The trapezoid rule has the error estimate
where 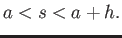 If interval
If interval ![$ [a,b]$](img180.png) is divided into
is divided into 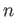 equal panels, show
that the error of the composite trapezoid rule is bounded by
equal panels, show
that the error of the composite trapezoid rule is bounded by
(c) Use the result in part (b) to determine the number of panels
sufficient to approximate
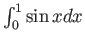 within to
within to
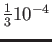 by using the composite trapezoid rule.
by using the composite trapezoid rule.
(a) (10 points) In the three point quadrature rule
choose 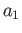 ,
, 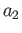 ,
, 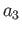 ,
, 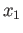 ,
, 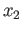 and
and 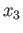 to maximize the
precision of the quadrature rule. (The result will be three-point
Gauss quadrature.)
to maximize the
precision of the quadrature rule. (The result will be three-point
Gauss quadrature.)
(b) (5 points)What is the degree of the resulting scheme?
Demonstrate this by showing the scheme correctly integrates a
polynomial of that degree, and that it does not integrate correctly
the polynomial of the degree of one order
higher.
Find
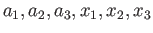 in
in
to maximize the precision of the quadrature. Find the error term of this quadrature.
- In class we have studied the two point Gauss quadrature
Calculate the error
term for this quadrature.
Hint Derivation is similar to calculation of the trapezoid
error term we did in class. You will need to express
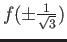 via
via 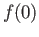 and its derivatives.
and its derivatives.
- In class we have studied two point Gauss quadrature. In this
problem you are to derive one point Gauss quadrature.
Consider the qudrature rule of the form
Choose 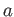 and
and 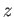 to maximize the order (accuracy) of the resulting
quadrature. What is the truncation order of this quadrature?
to maximize the order (accuracy) of the resulting
quadrature. What is the truncation order of this quadrature?
- Suppose that you have a tabular data, that is to say that the
function
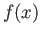 is given only on the
is given only on the 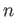 equidistant points
equidistant points 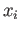 ,
,
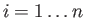 such that
such that 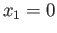 ,
, 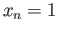 . Propose a way to
numerically evaluate
. Propose a way to
numerically evaluate
Chapter SEVEN
- Find an
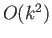 approximation of
approximation of 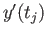 that utilizes
that utilizes
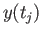 ,
,
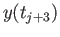 , and
, and
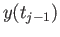 .
.
- You are producing a final project for your Master's
Degree and need to solve Initial Value Problem
numerically. You prefer to have accurate numerical
solution. Out of Forward Euler, Backward Euler,
Trapezoidal, Heun (RK2), and Runge-Kutta (RK4) method,
which method would you choose and why?
Consider RK2 (Heun's) method:
Show that this method is second order accurate, i.e. it finds exact
solution to the initial value problem
This can be done, for example, by showing that if at step 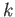 the
numerical solution is
the
numerical solution is
then at step 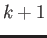 the
numerical solution is equal to
the
numerical solution is equal to
which agrees
with exact analytically solution
- Derive an
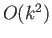 finite difference approximation to
finite difference approximation to 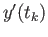 that
uses
that
uses
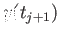 ,
,
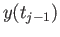 and
and
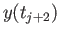 . Calculate the
truncation error term of the resulting finite difference approximation.
. Calculate the
truncation error term of the resulting finite difference approximation.
Find approximation of the first derivative 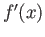 that uses
that uses 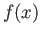 ,
,
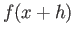 and
and 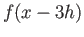 . What is the error term of your
approximation?
. What is the error term of your
approximation?
For the equation
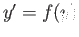 consider the following
numerical method
consider the following
numerical method
(a) Is this method explicit or implicit? Is it one-step or muti-step?
(b) Perform one step of the method for the equation
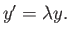
(c) Find the order of the method.
Consider the following  -step method for solving
-step method for solving
 |
(17) |
- What is the ”number of steps”
 for this method?
Is this method
explicit or implicit?
for this method?
Is this method
explicit or implicit?
- Determine
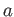 and
and 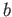 , for which the method has the
highest possible accuracy.
, for which the method has the
highest possible accuracy.
- Determine the order of the method of the
highest possible accuracy in (18).
- Determine the order of the method of the highest possible accuracy
in (18).
SOLUTION Method of undetermined coefficients, 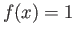 is satisfied
automatically,
is satisfied
automatically, 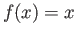 gives
gives 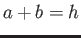 ,
,  gives
gives 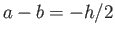 .
Solving equations we get
.
Solving equations we get
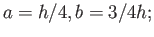 second order accurate
second order accurate
- Determine whether the method
with 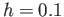 is stable for the equation
is stable for the equation
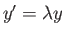 with
with
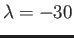 .
.
Suppose you want to solve numerically
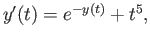 for
for
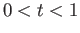 using 100 time steps (so,
using 100 time steps (so, 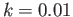 ). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
(a) Which method do you expect to finish the calculation the fastests?
Why?
(b) Which would be the second fastest method? Why?
(c) Which would be the most accurate method? Why?
(d) If stability is a concern, which method would be the best? Why?
This is general question. It is sufficient to give an answer
with out proof.
Consider the following initial value problem
The following algorithm is proposed for its numerical solution:
- Define the term stability for a numerical algorithm in the
context of initial value problems for ODE's.
- Determine if the above algorithm is stable, and if it is,
what restrictions if any is implied on the size of step size
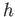 for stability.
for stability.
- List one advantage and one disadvantage of the above algorithm
over the Euler method.
Consider the following initial value
problem:
Using the Euler method with
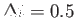 calculate
calculate 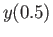 and
and
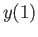 10 pt.
10 pt.
Is the proposed method numerically stable for the propsoed time step?
2 pt
Extra credit - 2 pt compare the result with the exact analytical
solution.
computer the solution of
for
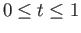 using 100 time steps (i.e. with
using 100 time steps (i.e. with
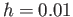 ). The methods to be tried are
). The methods to be tried are
- The 2nd order Taylor method
- RK4
- Trapezoid method
.
Please answer the following questions:
- Which one would you expect to complete the calculation the fastest? Why?
- Which one would you expect to complete the calculation last Why?
- Which one you expect to be more accurate? Why?
- If stability is a concern, which meshod should be used? Why?
Suppose you want to solve numerically
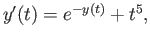 for
for
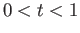 using 100 time steps (so,
using 100 time steps (so, 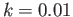 ). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
(a) Which method do you expect to finish the calculation the fastests?
Why?
(b) Which would be the second fastest method? Why?
(c) Which would be the most accurate method? Why?
(d) If stability is a concern, which method would be the best? Why?
IsHeun's method
stable for the equation
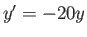 with
with 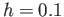 ?
?
Consider RK2 (Heun's) method:
Show that this method is second order accurate, i.e. it finds exact
solution to the initial value problem
This can be done, for example, by showing that if at step 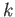 the
numerical solution is
the
numerical solution is
then at step 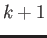 the
numerical solution is equal to
the
numerical solution is equal to
which agrees
with exact analytically solution
Consider the following initial value
problem:
Using Taylor second order scheme, calculate 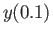 with
with
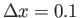 (i.e. calculate one time step).
(i.e. calculate one time step).
( 4 points) Compare the result with the exact analytical solution.
- State whether the following methods are (i) explicit or
implicit (ii) single step or multi-step (iii) selfstarting or not.
Cross out wrong statements and underline correct ones:
(i)explicit/implicit (ii)single step/multi-step (iii)selfstarting/not selfstarting.
(i)explicit/implicit (ii)single step/multi-step (iii)selfstarting/not selfstarting.
(i)explicit/implicit (ii)single step/multi-step (iii)selfstarting/not selfstarting.
- The Bernoulli equation is
- If the Forward Euler method is used to solve this equation,
what is the resulting finite difference equation (i.e. equation
expressing
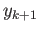 through
through 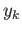 )?
)?
- If the trapezoid method is used to solve this equation,
what is the resulting finite difference equation?
- If the RK2 method is used, what is the resulting finite difference
equation?
- If the RK4 method is used, what is the resulting finite difference
equation?
Consider the fourth order RK method:
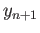 |
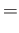 |
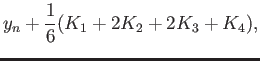 |
(18) |
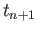 |
 |
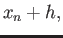 |
(19) |
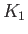 |
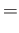 |
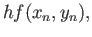 |
(20) |
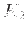 |
 |
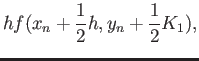 |
(21) |
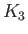 |
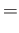 |
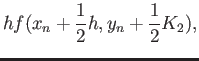 |
(22) |
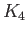 |
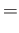 |
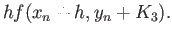 |
(23) |
Apply this RK4 method for solving the equation
with initial condition
and show that
the RK4 method is indeed at least fourth order accurate. This can be
done, for example, by showing that if at step 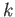 the numerical
solution is
the numerical
solution is
then at step 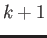 the numerical solution
is equal to
the numerical solution
is equal to
which agrees with exact
analytically solution
Consider the fourth order RK method:
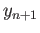 |
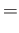 |
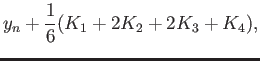 |
(24) |
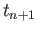 |
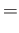 |
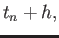 |
(25) |
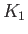 |
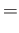 |
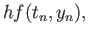 |
(26) |
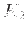 |
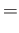 |
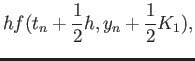 |
(27) |
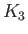 |
 |
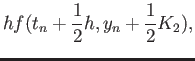 |
(28) |
 |
 |
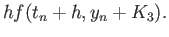 |
(29) |
Apply this RK4 method for solving the equation
and show that this method is indeed fourth order accurate. This can be done,
for example, by computing an amplification factor and comparing it to the
analytic value 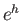 .
.
Chapter EIGHT
Set up the linear least squares problem for
fitting the model
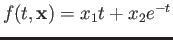 to the
four data points
to the
four data points 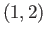 ,
, 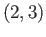 ,
, 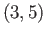 ,
, 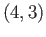 .
.
Set up and solve the linear least squares system
for the fitting the model function
to the three data points
(a) Suppose you would like to fit the data
points
by the fitting function
Find 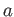 and
and 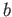 by setting up a linear (overdetermined)
least square problem and solving it.
by setting up a linear (overdetermined)
least square problem and solving it.
(b) Also calculate the residual.
Suppose you measure  as a function of
as a function of 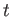 and you get the following:
and you get the following:
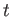 |
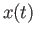 |
| 0 |
2 |
| 1 |
1 |
| 2 |
-2 |
| 3 |
-1 |
Suppose you would like to fit this data by
Find 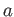 and
and 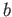 by setting up a linear (overdetermined)
least square problem and solving it. Also calculate the residal.
by setting up a linear (overdetermined)
least square problem and solving it. Also calculate the residal.
Consider the data
Apporximate this data by a constant, i.e. find  such that
such that
is a good fit for this data.
- Use least square method. As we have shown in class the least square
method minimizes the square of the second norm of a residual, i.e.
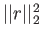 , where
, where
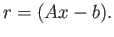
- Now minimize the fourth power of the fourth norm of a residual.
- Compare the results and explain the difference.
- Suppose that an experiment produced the following data:
You are to fit this data by using the linear fit
a Calculate the value of  which minimized the
square of the second norm
which minimized the
square of the second norm 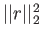 of the residual
of the residual
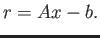
b Calculate 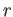 and
and 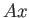 . Sketch
. Sketch
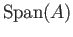 ,
, 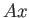 ,
, 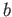 and
and 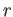 . Verify that
. Verify that
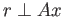 . Is it so on your graph?
. Is it so on your graph?
c Extra-credit, 5 points Obtain equation for  that minimizes
that minimizes 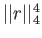 instead of
traditional
instead of
traditional 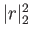 . Do not solve the resulting equation.
What are the advantages and disadvantages of using
. Do not solve the resulting equation.
What are the advantages and disadvantages of using 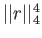 instead of
instead of
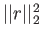 ?
?
Suppose that an experiment produced the following data:
You are to fit this data by using the linear fit
a Calculate the value of  which minimized the
square of the second norm
which minimized the
square of the second norm 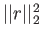 of the residual
of the residual
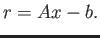
b Calculate 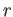 and
and 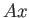 . Sketch
. Sketch
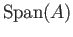 ,
, 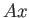 ,
, 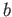 and
and 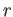 . Verify that
. Verify that
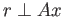 . Is it so on your graph?
. Is it so on your graph?
c Extra-credit, 5 points Obtain equation for  that minimizes
that minimizes 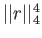 instead of
traditional
instead of
traditional 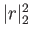 . Do not solve the resulting equation.
What are the advantages and disadvantages of using
. Do not solve the resulting equation.
What are the advantages and disadvantages of using 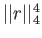 instead of
instead of
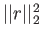 ?
?
- Let A be the
 identity matrix,
identity matrix,
Let  the vector
the vector
Find the least squares solution of
and calculate the residual and its 2-norm.
Let A be the 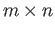 identity matrix
identity matrix
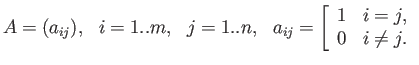 |
|
|
(30) |
Furthermore, let
Find the least squares solution of
and calculate the residual and its 2-norm.

 digits with base
digits with base  and
and  .
Subnormals are allowed.
.
Subnormals are allowed.
 and
number
and
number  and
and  ?
?
 and
and ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
and subnormals are allowed.
,
and subnormals are allowed.
![]() is a real number, and
is a real number, and ![]() is its
floating point representation, then the maximum possible relative error
in representing this number is given by
is its
floating point representation, then the maximum possible relative error
in representing this number is given by
![]() , precision
, precision ![]() and exponent range
and exponent range ![]() . In other words, each number in this system
can be represented as
. In other words, each number in this system
can be represented as
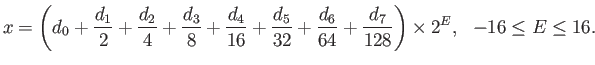
![]() so that all
real numbers from the interval are rounded to
so that all
real numbers from the interval are rounded to ![]() . That is, find
the smallest value of
. That is, find
the smallest value of ![]() and the largest vlue of
and the largest vlue of ![]() with
with ![]() so
that any number from the interval
so
that any number from the interval ![]() is rounded to the floating
point number
is rounded to the floating
point number ![]() . Assume double precision is used (53 binary digits).
. Assume double precision is used (53 binary digits).
![]() , that is, find the interval
, that is, find the interval ![]() that rounds to the floating point number
that rounds to the floating point number
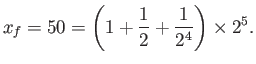
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() and
and
![]() for this system.
Assume rounding by chopping.
for this system.
Assume rounding by chopping.
![]() ? For example, how many floating point numbers are there
between 2 and 4?
? For example, how many floating point numbers are there
between 2 and 4?
![]() to
the next largest floating point number in this floating point
system?
to
the next largest floating point number in this floating point
system?
![]() to the next smallest floating point number in this floating point system?
to the next smallest floating point number in this floating point system?
![]() ?
?
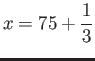
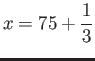
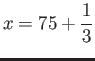
![]() using third degree Taylor polynomial
expanded about
using third degree Taylor polynomial
expanded about ![]() . Use this expansion to show that
. Use this expansion to show that
![]() to be 0.
to be 0.

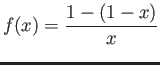
![]() , with
, with ![]() digits, and lower and upper values of the exponents of
digits, and lower and upper values of the exponents of ![]() ,
,
![]() . As we discussed in class, the number
. As we discussed in class, the number
![]() is not
representable in IEEE SP. What is the Floating Point Number that
precedes
is not
representable in IEEE SP. What is the Floating Point Number that
precedes
![]() ? In other words, find the largest Floating
Point Number that is less then
? In other words, find the largest Floating
Point Number that is less then
![]() .
.
![]() . In other words, find the smallest possible
positive number that is representable in this system. Write the
result in both binary and decimal format.
. In other words, find the smallest possible
positive number that is representable in this system. Write the
result in both binary and decimal format.
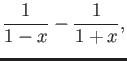
![]() it is difficult to calculate this
expresion accurately in floating point arithmetic?
it is difficult to calculate this
expresion accurately in floating point arithmetic?
![]() in part
a, the computation is more accurate in floating point system
in part
a, the computation is more accurate in floating point system
![]() will the computer claim that inequality
will the computer claim that inequality
![]() is true?
is true?
![]() will a computer claim that
will a computer claim that
![]() ?
?
![]() of
of ![]() is
exactly representable in this system. Why it is not possible? What
is the distance between two floating point numbers that is right
above and right below solution of
is
exactly representable in this system. Why it is not possible? What
is the distance between two floating point numbers that is right
above and right below solution of ![]() in this system?
in this system?
![]() and
and ![]() in this toy floating point systems are
such that
in this toy floating point systems are
such that
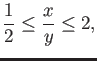
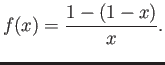
![]() ,
, ![]() ,
, ![]() ,
, ![]() . In single precision
floating point system write down the floating point number that
follows the number
. In single precision
floating point system write down the floating point number that
follows the number ![]() . (In other words, find minimal value of
. (In other words, find minimal value of
![]() , that is exactly representable in this floating point system.
, that is exactly representable in this floating point system.
![]() ,
, ![]() ,
, ![]() ,
, ![]() . What is the
smallest possible positive integer that is not a single precision
number?
. What is the
smallest possible positive integer that is not a single precision
number?
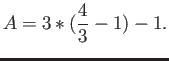
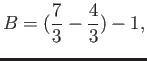
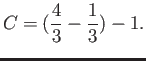
![]() , precision
, precision ![]() and exponent range
and exponent range ![]() I.e., in this system
any number can be written as
I.e., in this system
any number can be written as
![]()
![]() and
and ![]() such
that
such
that
![]() is minimal.
is minimal.
![]() by a machine number? What is the possible
relative error in representing
by a machine number? What is the possible
relative error in representing ![]() by a machine number?
by a machine number?
![]() and number
and number ![]() .
.
![]() and an exponent range of
and an exponent range of ![]() . What is the result of each of the following floating point
arithmetic operations?
. What is the result of each of the following floating point
arithmetic operations?
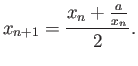
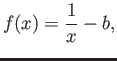
![]() requires computation of the derivative of
requires computation of the derivative of ![]() at each
iteration. Suppose that we instead replace the true derivative with a
constant value
at each
iteration. Suppose that we instead replace the true derivative with a
constant value ![]() , that is we use the iteration scheme
, that is we use the iteration scheme
![]() will this scheme be locally
convergent?
will this scheme be locally
convergent?
![]() to give a quadratic convergence?
to give a quadratic convergence?
![]() .
.
![]() ,
i.e. when
,
i.e. when
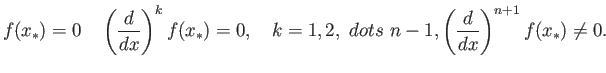
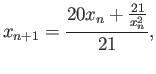
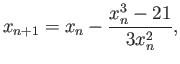
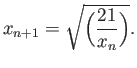
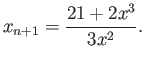
![]() ,
,
![]() and
and
![]() .
.
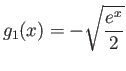
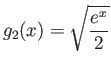
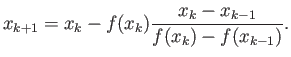
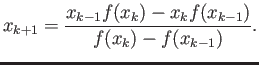
![]() were computed
using Matlab. What method was used (bisection, Newton or secant)? Make sure you explain in details
why it is the method you claim:
were computed
using Matlab. What method was used (bisection, Newton or secant)? Make sure you explain in details
why it is the method you claim:


 denotes the transposition
denotes the transposition




![]() be an
be an ![]() diagonal matrix with
all its diagonal entries equal to
diagonal matrix with
all its diagonal entries equal to ![]() .
.
![]() ?
?
![]() ?
?
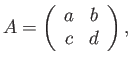
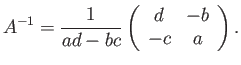
![\begin{displaymath}A =
\left[
\begin{array}{rr}
1 & -2 \\
-2 & 3
\end{array}\right]
\end{displaymath}](img265.png)
![]() such that
such that
![]()
![\begin{displaymath}
A =
\left[
\begin{array}{rr}
-1 & 1 \\
0 & \alpha
\end{a...
... \
b =
\left[
\begin{array}{rr}
1 \\
1
\end{array}\right] \end{displaymath}](img269.png)
![]() , if any, the matrix
, if any, the matrix ![]() will be
ill-conditioned?
will be
ill-conditioned?
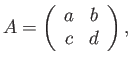
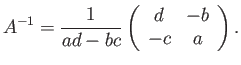
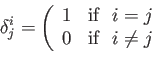
![]() matrix
matrix ![]() defined as
defined as
![]() is a diagonal matrix with diagonal entries being equal to
is a diagonal matrix with diagonal entries being equal to
![\begin{displaymath}
{\bf A=}\left[
\begin{array}{rrr}
2 & -4 & 2 \\
1 & 0 & 5 \\
2 & -2 & 2
\end{array}\right]
\end{displaymath}](img277.png)
![\begin{displaymath}
{\bf A=}\left[
\begin{array}{rrr}
5 & 6 & 7 \\
10 & 20 & 23 \\
15 & 50 & 58
\end{array}\right]
\end{displaymath}](img279.png)
![\begin{displaymath}
b =\left[
\begin{array}{r}
6\\
13\\
23
\end{array}\right]
\end{displaymath}](img280.png)
![\begin{displaymath}
{\bf A=}\left[
\begin{array}{rrr}
1 & 3 & 5 \\
2 & 9 & 15 \\
2 & 18 & 37
\end{array}\right]
\end{displaymath}](img16.svg)
![\begin{displaymath}
b =\left[
\begin{array}{r}
22\\
65\\
149
\end{array}\right]
\end{displaymath}](img17.svg)
![]() factorization of
factorization of ![]() .
.
![]() decomposition to solve (9).
decomposition to solve (9).
![\begin{displaymath}
{\bf B=}\left[
\begin{array}{rrr}
1 & 0 & 0 \\
2 & 1 & 0 \\
3 & 2 & 1
\end{array}\right]
\end{displaymath}](img18.svg)
 by representing the matrix as a
product of two elementary Gauss elimination matrices.
by representing the matrix as a
product of two elementary Gauss elimination matrices.
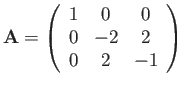
![]() ,
,


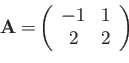
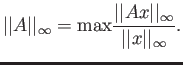
![]() norm through the
vector norm to proove that the
norm through the
vector norm to proove that the ![]() norm of a matrix is a
maximum absolute row sum.
norm of a matrix is a
maximum absolute row sum.
![]() matrices.
matrices.
![]() matrices.
matrices.
![]() is small. The system has two approximate
solutions
is small. The system has two approximate
solutions
![]() and
and
![]() Find the norms of the respective
residuals. Which one is smaller? Find the condition number of the
matrix. Explain, why you should not use residuals in this case to
determine the quality of a solution.
Find the norms of the respective
residuals. Which one is smaller? Find the condition number of the
matrix. Explain, why you should not use residuals in this case to
determine the quality of a solution.
![\begin{displaymath}
\left[
\begin{array}{rr}
a & b \\
c & d
\end{array}\right]...
...left[
\begin{array}{rr}
d & -b \\
-c & a
\end{array}\right]
\end{displaymath}](img298.png)
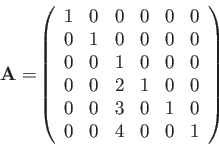

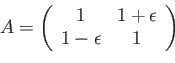
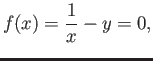
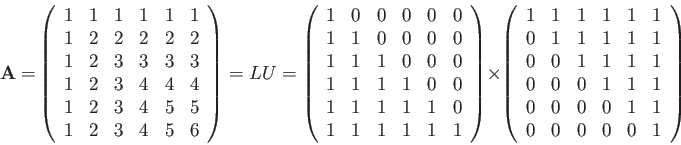
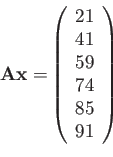
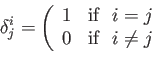
![]() matrix
matrix ![]() defined as
defined as
![]() is a diagonal matrix with diagonal entries being equal to
is a diagonal matrix with diagonal entries being equal to
 , and eigenvectors
, and eigenvectors
 . Let the
. Let the
 and same
eigenvectors
and same
eigenvectors
 . What are eigenvectors and eigenvalues
of the matrix
. What are eigenvectors and eigenvalues
of the matrix  given by
given by

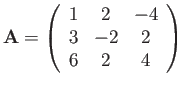
![]() . For this matrix, what Eigenvalue would the
power method converge to? Why?
. For this matrix, what Eigenvalue would the
power method converge to? Why?
![]() matrix
matrix

![]() is a symmetric
is a symmetric ![]() matrix with
eigenvalues
matrix with
eigenvalues
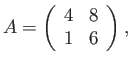
![]() .
.
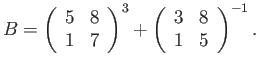
![]() explicitly.
explicitly.
![]() so that the given function is a natural cubic
spline from
so that the given function is a natural cubic
spline from
![]() .
.
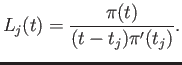
![]() for
for
![]()
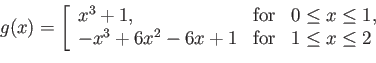
![]() quadratic polynomials that
interpolate these
quadratic polynomials that
interpolate these ![]() points, such that the resulting piece wise
quadratic polynomial has continuous first derivative. How many
additional conditions are required to make a square system for the
coefficients of this quadratic spline?
points, such that the resulting piece wise
quadratic polynomial has continuous first derivative. How many
additional conditions are required to make a square system for the
coefficients of this quadratic spline?
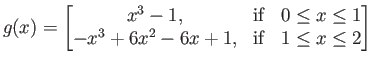
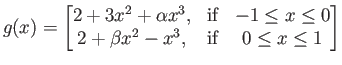
![]() between the nodes 0,
between the nodes 0, ![]() and
and ![]() .
.
![]() data points. Explain the
difference between interpolation and approximation. What Is the difference
between an interpolating polynomial of degree
data points. Explain the
difference between interpolation and approximation. What Is the difference
between an interpolating polynomial of degree ![]() and an approximating
polynomial of the same degree
and an approximating
polynomial of the same degree ![]() ?
?
![]() between the nodes
between the nodes ![]() .
.
![]() .
.
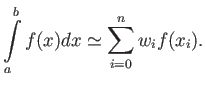
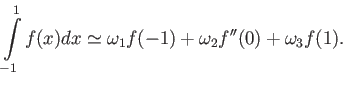
![]() to maximize the precision of the quadrature. What is the
order of the resulting quadrature?
to maximize the precision of the quadrature. What is the
order of the resulting quadrature?
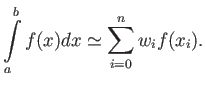
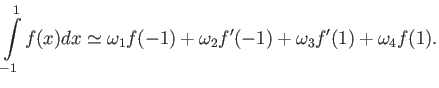
![]() ,
, ![]() ,
, ![]() and
and
![]() .
.
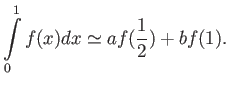
![]() and
and ![]() to maximize the accuracy of the resulting
quadrature. Calculate the truncation error of the resulting
quadrature.
to maximize the accuracy of the resulting
quadrature. Calculate the truncation error of the resulting
quadrature.
![]() :
:
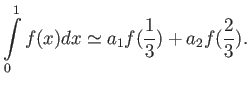
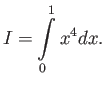
![]() on only three points,
on only three points,
![]() ,
,
![]() and
and ![]() .
.
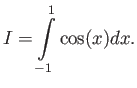
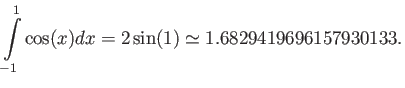
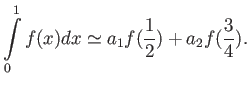
![]() if the standard 3-point Gaussian rule is given by
if the standard 3-point Gaussian rule is given by

![$\displaystyle \int_{a}^{a+h}g(x)dx=\frac{h}{2}\left[ g(a)+g(a+h)\right] -\frac{1}{12}%
h^{3}g^{\prime \prime }(s)
$](img399.png)
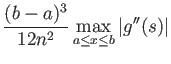
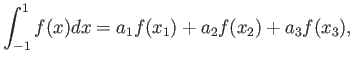
![]() in
in
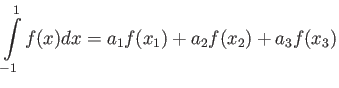
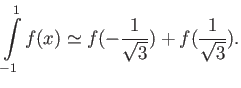
![]() via
via ![]() and its derivatives.
and its derivatives.
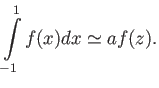
![]() and
and ![]() to maximize the order (accuracy) of the resulting
quadrature. What is the truncation order of this quadrature?
to maximize the order (accuracy) of the resulting
quadrature. What is the truncation order of this quadrature?
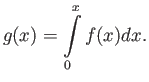
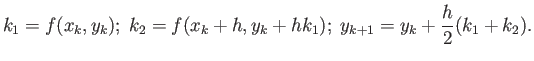
![]() the
numerical solution is
the
numerical solution is ![]() that uses
that uses ![]() ,
,
![]() and
and ![]() . What is the error term of your
approximation?
. What is the error term of your
approximation?
![]() consider the following
numerical method
consider the following
numerical method
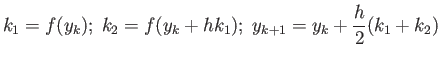
![]() -step method for solving
-step method for solving
![]()
![]() is satisfied
automatically,
is satisfied
automatically, ![]() gives
gives ![]() ,
, ![]() gives
gives ![]() .
Solving equations we get
.
Solving equations we get
![]() second order accurate
second order accurate
![$\displaystyle y_{k+1}=y_{k}+hf(t_{k},y_{k})+\frac{h^{2}}{2}\left[ \frac{\partia...
...{\partial t}+f(t_{k},y_{k})\frac{\partial f(t_{k},y_{k}%
)}{\partial y}\right]
$](img447.png)
![]() for
for
![]() using 100 time steps (so,
using 100 time steps (so, ![]() ). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
![$\displaystyle y_{n+1} = y_n + \frac{h}{2}\left[ f(t_n,y_n)+f(t_{n+1}, y_{n+1})\right].$](img455.png)
![]() calculate
calculate ![]() and
and
![]() 10 pt.
10 pt.
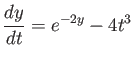
![]() for
for
![]() using 100 time steps (so,
using 100 time steps (so, ![]() ). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.
). The method to be tried
are (i) the Euler method (ii) the backward Euler method (iii) the trapezoidal method (iv) the RK2 (Heun) method (v) the RK4 method.


![]() the
numerical solution is
the
numerical solution is 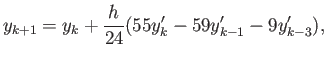
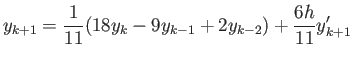
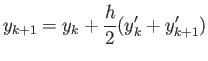
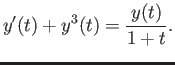
![]() to the
four data points
to the
four data points ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() as a function of
as a function of ![]() and you get the following:
and you get the following:
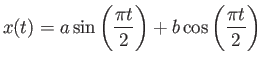
![]() such that
such that
![]() which minimized the
square of the second norm
which minimized the
square of the second norm ![]() of the residual
of the residual
![]()
![]() and
and ![]() . Sketch
. Sketch
![]() ,
, ![]() ,
, ![]() and
and ![]() . Verify that
. Verify that
![]() . Is it so on your graph?
. Is it so on your graph?
![]() that minimizes
that minimizes ![]() instead of
traditional
instead of
traditional ![]() . Do not solve the resulting equation.
What are the advantages and disadvantages of using
. Do not solve the resulting equation.
What are the advantages and disadvantages of using ![]() instead of
instead of
![]() ?
?
![]() which minimized the
square of the second norm
which minimized the
square of the second norm ![]() of the residual
of the residual
![]()
![]() and
and ![]() . Sketch
. Sketch
![]() ,
, ![]() ,
, ![]() and
and ![]() . Verify that
. Verify that
![]() . Is it so on your graph?
. Is it so on your graph?
![]() that minimizes
that minimizes ![]() instead of
traditional
instead of
traditional ![]() . Do not solve the resulting equation.
What are the advantages and disadvantages of using
. Do not solve the resulting equation.
What are the advantages and disadvantages of using ![]() instead of
instead of
![]() ?
?
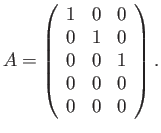
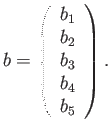
![]() identity matrix
identity matrix