- A30: General introduction, motivation for numerical computing,
strategies and phylosophy of in NC, absolute and relative error,
computational and propagated data error, truncation and rounding
error. pp 1-12
- S2: Rounding error (cont). Forward and backward error,
examples. Condition number and properties of Condition
number. Computer arithmetics.
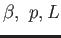 and
and 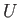 . Total number of
numbers, OFL and UFL pp 13-18.
. Total number of
numbers, OFL and UFL pp 13-18.
- S9: Rounding, Subnormals, Inf and NaN, Floating point
arithmetics,
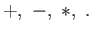 , cancellations. Matlab introduction
and Matlab demonstration of infinite series sum. pp 19-27.
, cancellations. Matlab introduction
and Matlab demonstration of infinite series sum. pp 19-27.
- S13 First Quiz. Linear Algebra
Linear Algebraic systems, Existence and Uniqueness, simple
examples, matrices and vectors: 1,2 and
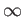 norms.
Cramer rule for solving linear systems. Matlab
demonstration: matrices, their inverses, transposed, condition number,
norms, determinant, operations on matrices, code for implementing
Cramer rule. pages 49-56
norms.
Cramer rule for solving linear systems. Matlab
demonstration: matrices, their inverses, transposed, condition number,
norms, determinant, operations on matrices, code for implementing
Cramer rule. pages 49-56
- S16 Properties of norms, 1,2 and
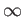 norms for vectors. Matrix
norms. Condition number for a matrix.
Geometrial interpretation of a
condition number. Error Estimates, residual.pages 56-63
norms for vectors. Matrix
norms. Condition number for a matrix.
Geometrial interpretation of a
condition number. Error Estimates, residual.pages 56-63
- S20
Theory: premultiplying and postmultiplying systems of linear
equations, diagonal scaling, triangular matrices, upper- and
lower-diagonal matrices, forward and backward substitutions,
elementary elimination matrices and their properties. pages 64-68
- S23 Gauss eliminations and LU decomposition, examples, partial
and complete pivoting, Cholesky factorisation. 68-75,78-79,84-86
- S26 Linear Least Squares, set up of a problem, motivations
and examples, overdetermined systems, Normal equations, geometric
interpretation.
- S29 Geometrical interpretation (cont), orthogonal projectors,
pseudoinverse and condition number, error estimates, data fitting,
augmented systems.
- Orthogonal transformations, QR factorization, orthogonal
basis, Householder transformation,
- Givens rotations. GM-ortho-normalization.
- Midterm?
- Eigenvalues and
Eigenvectors Eigenvalue and Eigenfunctions - definitions, examples,
problem transofrmation. (direct, normalized and inverse) power
iterations, deflation method.
- O18 Nonlinear system of equations. Bisection method.
- O21 Fixed point iterations. Newton method. Estimating the
convergence rate.
- O25 Secant method. Linear and quadratic interpolation. Inverse
interpolation. Linear Fractional interpolation.
- O28 Generalization to N dimensions. Fixed point iterations.
Newton method, simplified formulation. General formulation, Jacobians,
etc. Stopping criteria. Interpolation. Interpolation, general
formulation. Monominal interpolation. Scaled monomials.
- N1 Scaled monomials. Lagrange interpolation. Newton
interpolation: triangular system, Incremental Newton interpolation.
- N4 Incremental Newton interpolation. Divided
differences. Orthogonal Polynomials. Legendre and Chebyshev.
Intrpolating continious funcitions.Piecewise polynomial, Hermite
interpolation and Cubic splines.
- . N8 Cubic splines. Review of Splines Numerical
Intergration. Introduction to numerical integration. Quadrature rules
that is based on Lagrange interpolation. “Baby” quadrature
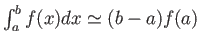 . Error estimate of this quadrature rule.
. Error estimate of this quadrature rule.
- N11 Midpoint method. Error estimate for midpoint. Trapezoid
method. Error Estimate for trapezoid method.
item N15. Simpson
method as a weigted average of Trapezoid and Midpoint. Method of
undetermined coefficients. Composite and progressive quadratures.
- N15 Adaptive quadratures. Gauss quadratures. Review for midterm
- N18 ???
- N Midterm
- N29 Gauss quadrature. Derivation of Gauss quadratures using
orthonormal polynomials. Improper and singular integrals.
- Lecture on Numerical differentiating
- D2 Numerical Methods for Solving ODE's Stable, unstable
and Asymptotically stable ODE's. Numerical stability. Forward Euler method.
- D6 Backward Euler method, Implicit methods, Trapezoid method,
Taylor method, Runge-Kutta methods. Multi-step methods.
- D9 Concluding remarks