- Chapter 1. Introduction, Errors, representing numbers
in a computer. Numerical errors.
- Floating Point Arithmetic, machine precision, NaN, Inf,
overflow, underflow
- Arithmetical operations in Floating Points. Chapter 2
Solving nonlinear equations, rate of convergence, Bisection method,
fixed point iterations.
- Newton Method, rate of convergence.
- Stopping criteria, hybrid methods, overview. Secant Method
3 Chapter
3, Linear system of equations
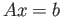. Existence and uniqueness of
solutions.
- S19 Forward and Backward substitution, Gauss Elementary elimination
matrices and LU decomposition. Partial and Complete pivoting.
- F24 Vector and Matrix norms. Condition number of a matrix. Properties
of vector and matrix norms. Properties of condition numbers.
- F28 Absolute and relative residual. Error Estimates. Newton method for
solving nonlinear system of equations.
- S29
- O3
- O6
- O11
- O13 Introduction to interpolation. Formulation of a problem, monomial
interpolation.
- O17 Interpolation - Lagrange interpolation, wiggles, Piece wise linear
interpolation.
- O20
- O24 Midterm
- O27
- O31
- N3
- N7
- N10
- N14
- N17
- N21 Midterm
- N28
- D1
- D5 Matlab Lab
- D8 concluding Remarks
