The dispersive interacting waves in Fermi-Pasta-Ulam (FPU) chains of
particles in
thermal equilibrium are studied from both
statistical and wave resonance perspectives. It is shown that, even
in a strongly nonlinear regime, the chain in thermal equilibrium can
be effectively described by a system of weakly interacting
renormalized nonlinear waves that possess (i) the
Rayleigh-Jeans distribution and (ii) zero correlations between
waves, just as noninteracting free waves would. This renormalization
is achieved through a set of canonical transformations. The
renormalized linear dispersion of these renormalized waves is
obtained and shown to be in excellent agreement with numerical
experiments. Moreover, a dynamical interpretation of the
renormalization of the dispersion relation is provided via a
self-consistency, mean-field argument. It turns out that this
renormalization arises mainly from the trivial resonant wave
interactions, i.e., interactions with no momentum exchange.
Furthermore, using a multiple time-scale, statistical averaging
method, we show that the interactions of near-resonant waves give
rise to the broadening of the resonance peaks in the frequency
spectrum of renormalized modes. The theoretical prediction for the
resonance width for the thermalized
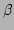
-FPU chain is found to be
in very good agreement with its numerically measured value.