- ... taken.1
-
It is easily to extend
the analysis to the infinite Fourier space,
 .
In this case, the full joint PDF would still have
to be defined as a
.
In this case, the full joint PDF would still have
to be defined as a 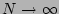 limit of an
limit of an
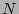 -mode PDF, but this limit would have to be taken
in such a way that both
-mode PDF, but this limit would have to be taken
in such a way that both 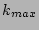 and the density of the Fourier modes
tend to infinity simultaneously.
and the density of the Fourier modes
tend to infinity simultaneously.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scales.2
- Hereafter we omit superscript
 in the
in the 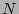 -mode objects if it does not lead to a confusion.
-mode objects if it does not lead to a confusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
respectively. 3
- This technique provides a useful
classification method but not a complete mathematical description of
the terms involved.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... means4
- In the present paper we consider only spatially homogeneous wave
turbulence fields. In spatially homogeneous fields, due to momentum
conservation, there is no coupling to the zero mode
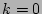 because such
coupling would violate momentum conservation. Therefore if one of the
arguments of the interaction matrix element
because such
coupling would violate momentum conservation. Therefore if one of the
arguments of the interaction matrix element 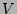 is equal to zero, the
matrix element is identically zero. That is to say that for any
spatially homogeneous wave turbulence system
is equal to zero, the
matrix element is identically zero. That is to say that for any
spatially homogeneous wave turbulence system
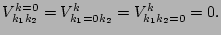
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... factors.5
- There is of course also a possibility
that
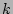 couples simultaneously to both indices in a pair, but
this contribution contains
couples simultaneously to both indices in a pair, but
this contribution contains 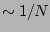 less terms and, therefore,
should be ignored.
less terms and, therefore,
should be ignored.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
graphs. 6
- The only possibility of the double internal coupling
would be in the last graph via joining
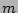 with
with 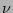 and
and 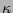 with
with 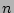 , but this would mean
, but this would mean 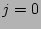 because of the
because of the 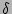 -symbols
and, therefore, this term is nill.
-symbols
and, therefore, this term is nill.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.